题目内容
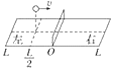
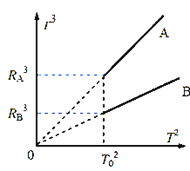
【题目】如图甲所示，一个重力不计的弹性绳水平放置，a、b、c是弹性绳上的三个质点。现让质点a从t＝0时刻开始在竖直面内做简谐运动，其位移随时间变化的振动方程为x＝20sin（5πt）cm，形成的简谐波同时沿该直线向ab和ac方向传播。在t1＝0.8s时刻质点b恰好第一次到达正向最大位移处，a、b两质点平衡位置间的距离L1＝1.4m，a、c两质点平衡位置间的距离L2＝0.6m。求：
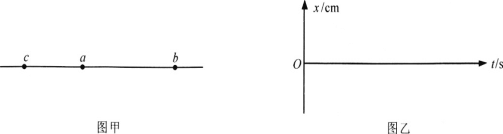
①此横波的波长和波速；
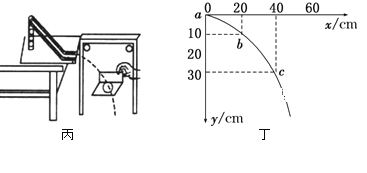
②在图乙中画出质点c从t＝0时刻开始位移随时间变化的振动图像（要求写出计算过程）。
【答案】①
②
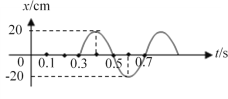
【解析】
根据“位移随时间变化的振动方程为x＝20sin（5πt）cm”、“在t1＝0.8s时刻质点b恰好第一次到达正向最大位移处”、“此横渡的波长和波速”、“在图乙中画出质点c从t＝0时刻开始位移随时间变化的振动图像”可知，本题考查机械波的振动方程、形成和传播、振动图像，根据机械波的振动方程可求周期；根据位移、波速、周期的关系，可求波速和波长；根据位移波速关系，可求质点C开始振动的时间，画出振动图像。
①由质点
位移随时间变化的振动方程可知：
（1）
设质点a振动产生的机械波的波长为
，波速为v，由题意可得：
（2）
可得：
（3）
据波长、波速和周期的关系，可得该波的波长
解得：
（4）
②设波由点传播到
点所用时间为
，之前质点处于静止状态。
（5）
从
开始经过
后，质点c即将向上振动，其振幅为
，振动周期和振源a的周期相等，为
，所以质点c的振动图像为下图所示：
练习册系列答案
相关题目
