题目内容
13．
如图所示，水平传送带水平段长L=6m，两皮带轮直径D均为0.2m，距地面高H=5m，与传送带等高的光滑水平台上有一小物块以v0=5m/s的初速度滑上传送带，物块与传送带间动摩擦因数μ=0.2，g取10m/s2．若皮带轮顺时针以角速度ω=60rad/s转动，求滑块到B端后做平抛运动的水平距离．
分析 对加速过程，先根据牛顿第二定律列式求解加速度，根据运动学公式求解加速距离，判断平抛的初速度；对平抛过程，根据分位移公式列式求解．
解答 解：皮带轮顺时针以角速度ω=60rad/s转动，线速度为：v=rω=$\frac{0.2m}{2}×$60rad/s=6m/s
物体的加速过程的加速度为：a=μg=2m/s2
加速距离为：S=$\frac{{v}^{2}-{v}_{0}^{2}}{2a}$=$\frac{{6}^{2}-{5}^{2}}{2×2}$=2.75m＜L=6m
故物体离开传送带的速度为6m/s；
对平抛过程，有：
水平方向：x=vt
竖直方向：H=$\frac{1}{2}g{t}^{2}$
解得：x=v$\sqrt{\frac{2H}{g}}$=6×$\sqrt{\frac{2×5}{10}}$=6m
答：滑块到B端后做平抛运动的水平距离为6m．
点评 本题关键是明确滑块的受力情况和运动情况，然后分加速、匀速和平抛过程列式求解，基础题目．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
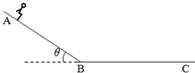滑雪运动是把滑雪板装在靴底上在雪地上进行速度、跳跃和滑降的竞赛运动．滑雪运动中当滑雪板相对雪地速度较大时，会把雪内的空气逼出来，在滑雪板与雪地间形成一个暂时的“气垫”，从而大大减小雪地对滑雪板的摩擦．然而当滑雪板相对雪地速度较小时，与雪地接触时间超过某一值就会陷下去，使得它们间的摩擦力增大．假设滑雪者的速度超过8m/s时，滑雪板与雪地间的动摩擦因数就会由μ1=0.25变为μ2=0.125．一滑雪者从倾角θ=37°的坡顶A处由静止开始自由下滑，滑至坡底B（B处为一光滑小圆弧）后又滑上一段水平雪地，最后停在C处，如图所示．不计空气阻力，已知坡长L=30.5m，水平雪地与坡面雪地的粗糙程度相同．取g=10m/s2，sin37°=0.6，cos37°=0.8，求：
4．关于弹力，下列说法正确的是（ ）
| A． | 相互接触的物体间一定有弹力； | |
| B． | 弹簧的弹力总跟弹簧的伸长量成正比 | |
| C． | 只有发生弹性形变的物体，才会对跟它接触的物体产生弹力 | |
| D． | 只有受弹簧作用的物体，才会受到弹力 |
如图所示，在竖直平面内固定一半径R为2m、圆心角为106°的光滑圆弧轨道BEC，其中E点是最低点．在B、C两端平滑、对称地连接长度均为2.5m的AB、CD两段粗糙直轨道，直轨道上端A、D与最低点E之间的高度差h均为2.8m．现将质量为0.01kg的小物块由A点静止释放，物块与直轨道间的动摩擦因数均为0.4．（g取10m/s2，sin53°=0.8，cos53°=0.6），忽略空气阻力的影响，求：
18．关于曲线运动，下列说法正确的是（ ）
| A． | 一定是变速运动 | B． | 一定是变加速运动 | ||
| C． | 一定不是匀变速运动 | D． | 以上说法都错 |