题目内容
某星球的质量是地球的2倍,其半径是地球的
.若不计其他星球的影响,该星球的第一宇宙速度是地球的第一宇宙速度的
| 1 | 2 |
2
2
倍,某物体在该星球表面上所受重力是在地球表面上所受重力的8
8
倍.分析:第一宇宙速度是卫星绕星近表面速度,根据地球对卫星的万有引力提供向心力求解.根据万有引力近似等于重力,求出重力之比.
解答:解:设地球质量为M1,半径为R1;某星球的质量为M2,半径为R2
由万有引力定律得:G
=m
可得:第一宇宙速度v=
代入解得,该星球与地球第一宇宙速度之比为2:1.
故星球的第一宇宙速度是地球上第一宇宙速度的2倍.
由重力等于万有引力得:G重=G
则得:
=
?
=
×
=8
故答案为:2;8.
由万有引力定律得:G
| Mm |
| R2 |
| v2 |
| R |
可得:第一宇宙速度v=
|
代入解得,该星球与地球第一宇宙速度之比为2:1.
故星球的第一宇宙速度是地球上第一宇宙速度的2倍.
由重力等于万有引力得:G重=G
| Mm |
| R2 |
则得:
| G星 |
| G地 |
| M星 |
| M地 |
| R地2 |
| R星2 |
| 2 |
| 1 |
| 4 |
| 1 |
故答案为:2;8.
点评:对于卫星类型问题,关键是要建立物理模型,运用万有引力定律和向心力知识,加上数学变换来求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
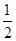 。若不计其他星球的影响,该星球的第一宇宙速度是地球的第一宇宙速度的________倍,某物体在该星球表面上所受重力是在地球表面上所受重力的__________倍。
。若不计其他星球的影响,该星球的第一宇宙速度是地球的第一宇宙速度的________倍,某物体在该星球表面上所受重力是在地球表面上所受重力的__________倍。