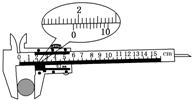
题目内容
7.某行星表面没有气体,在它的表面附近作匀速圆周运动的卫星的环绕周期为T,如果宇航员在这个行星地面上以初速度V0竖直向上抛出一石块,石块经过时间t再次回到宇航员手中.已知万有引力恒量为G,求该行星的质量及平均密度?分析 在天上飞就列万有引力提供向心力的公式,在地面上求出重力加速度,列黄金代换的公式,密度ρ=$\frac{M}{\frac{4}{3}π{R}^{3}}$,联立求解即可.
解答 解:卫星在表面附近,可认为其轨道半径r等于行星半径R,设行星质量M,卫星质量m,
由万有引力提供向心力得:G$\frac{Mm}{{R}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}R$,
解得:GM=$\frac{4{π}^{2}{R}^{3}}{{T}^{2}}$…①
在星球上:设行星表面重力加速度为g,由:V0=g•$\frac{t}{2}$得:g=$\frac{2{V}_{0}}{t}$,
由黄金代换:GM=gR2
得:GM=$\frac{2{V}_{0}{R}^{2}}{t}$…②
密度ρ=$\frac{M}{\frac{4}{3}π{R}^{3}}$…③
联立①②③解得:M=$\frac{{V}_{0}^{3}{T}^{4}}{2G{π}^{4}{t}^{3}}$
密度ρ=$\frac{3{T}^{2}}{8G{π}^{5}}$
答:该行星的质量为:$\frac{{V}_{0}^{3}{T}^{4}}{2G{π}^{4}{t}^{3}}$;平均密度为$\frac{3{T}^{2}}{8G{π}^{5}}$.
点评 万有引力与航天的题目,在天上就列万有引力提供向心力的公式,在地面上就列黄金代换的公式,是处理这类题目的通法.

练习册系列答案
相关题目
17.我国研制并成功发射的“嫦娥二号”探测卫星,在距月球表面高度为h的轨道上做匀速圆周运动,运行的周期为T.若以R表示月球的半径,则( )
| A. | 卫星运行时的线速度为$\frac{2πR}{T}$ | |
| B. | 卫星运行时的向心加速度为$\frac{4{π}^{2}(R+h)}{{T}^{2}}$ | |
| C. | 月球的第一宇宙速度为$\frac{2π\sqrt{R(R+h)^{3}}}{TR}$ | |
| D. | 物体在月球表面自由下落的加速度为$\frac{{4{π^2}R}}{T^2}$ |
18.1825年,瑞士物理学家德拉里夫的助手科拉顿将一个螺线管与电流计相连.为了避免强磁性磁铁影响,他把电流计放在另外一个房间,当他把磁铁投入螺线管中后,立即跑到另一个房间去观察,关于科拉顿进行的实验.下列说法正确的是( )
| A. | 在科拉顿整个操作过程中,电流计不发生偏转 | |
| B. | 将磁铁投入螺线管瞬间,电流计发生偏转,但科拉顿跑过去观察时,电流计已不再偏转 | |
| C. | 科拉顿无法观察到电流计偏转的原因是当时电流计灵敏度不够 | |
| D. | 科拉顿无法观察到电流计偏转的原因是导线过长,电流过小 |
15.一个质点分别受到下列四组共点力的作用,一定使质点产生加速度的一组共点力是( )
| A. | 25N,15N,40N | B. | 10N,15N,20N | C. | 10N,20N,40N | D. | 2N,4N,6N |
19.质量为m1、m2的甲乙两物体间的万有引力,可运用万有引力定律F=G$\frac{{m}_{1}{m}_{2}}{{r}_{2}}$计算.则下列说法正确的是( )
| A. | 当两物体间的距离小到接近零时,它们之间的万有引力将是无穷大 | |
| B. | 若只将第三个物体放在甲乙两物体之间,甲乙之间的万有引力会改变 | |
| C. | 甲对乙的万有引力的大小与乙对甲的万有引力的大小总相等 | |
| D. | 若m1>m2,甲对乙的万有引力大于乙对甲的万有引力 |
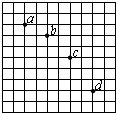 在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.若用一张印有小方格的纸记录轨迹,小方格的边长为5cm,小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的大小为v0=1.4m/s(g取9.8m/s2).
在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.若用一张印有小方格的纸记录轨迹,小方格的边长为5cm,小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的大小为v0=1.4m/s(g取9.8m/s2).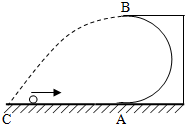 如图,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,(忽略空气阻力)则
如图,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,(忽略空气阻力)则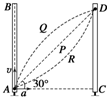 如图所示,竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以速度v匀速上浮.红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀减速向右运动,则蜡块的轨迹可能是( )
如图所示,竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以速度v匀速上浮.红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀减速向右运动,则蜡块的轨迹可能是( )