Question

【题目】如图所示，一固定的足够长的竖直气缸有一大一小两个同轴圆筒组成，两圆筒中各有一个活塞，已知大活塞的质量为，横截面积为，小活塞的质量为，横截面积为，两活塞用刚性轻杆连接，活塞的厚度可以忽略，间距保持为，气缸外大气压强为。初始时大活塞与小圆筒底部相距，两活塞间封闭气体的温度为，现气缸内气体温度缓慢改变，活塞缓慢移动，忽略两活塞与气缸壁之间的摩擦，重力加速度g取10m/s2。求：

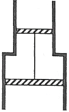
(1)在大活塞与小圆筒底部接触前的瞬间，缸内封闭气体的温度和压强；

(2)要保证缸内封闭的气体不漏气，缸内封闭气体的最高温度。

Answer 1

【答案】(1) T2=330K , (2) T3=660K

【解析】（i）设初始时气体体积为V1，在大活塞与小圆筒底部刚接触时，缸内封闭气体的体积为V2，温度为T2，由题给条件得： ;

在活塞缓慢上移的过程中，缸内气体的压强不变。

由盖–吕萨克定律有：

联立方程解得：T2=330K

用pl表示缸内气体的压强，由力的平衡条件得：

解得：

（ii）当小活塞与大圆筒顶部刚接触时温度达到最高，可保证缸内封闭的气体不漏气，设此时温度为T3，体积为V3，压强仍然不变，由题意

由盖–吕萨克定律，有：

联立上式并代入题给数据得T3=660K

点睛; 本题考查了求气体的温度与压强，分析清楚气体状态变化过程、找到气体的状态变化参量，应用盖吕萨克定律与查理定律即可正确解题．