题目内容
9.如图1所示,一端带有定滑轮的长木板上固定有甲、乙两个光电门,与之相连的计时器可显示带有遮光片的小车在其间的运动时间,与跨过定滑轮的轻质细绳相连的传感器能显示挂钩处所受的拉力,不计空气阻力及一切摩擦.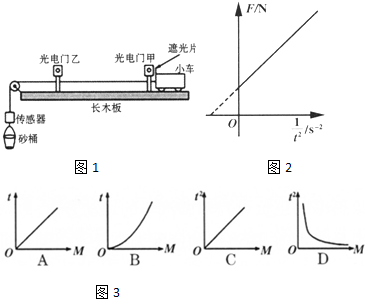
(1)在探究“合外力一定时,加速度与质量的关系”时要使实验成功,操作中必须满足小车与滑轮间的细绳与长木板平行;此实验中不需要(填“需要”或“不需要”)砂和砂桶的总质量m远小于小车和砝码的总质量M.
(2)实验时,先测出小车和砝码的总质量M,再让小车从靠近光电门甲处由静止开始运动,读出小车在两光电门间的运动时间t.改变M,测得多组M、t的值,建立坐标系描点画出图线.下列能直观得出“合外力一定时,加速度与质量成反比”的图线是图3中的C(单选题)
(3)若实验中抬高长木板的左端,使小车从靠近光电门乙处由静止开始运动,读出传感器的示数F和小车在两光电门之间的运动时间t,改变木板倾角测得多组数据,得到的F-$\frac{1}{{t}^{2}}$的图线如图2示,若两光电门的距离L=0.80m,砂和砂桶的总质量m=0.34kg,取g=9.8m/s2,则图线的斜率为0.54kg•m(小数点后保留两位有效数字);若小车与长木板间的摩擦不能忽略,测得的图线斜率将不变 (填:变大、变小、不变).
分析 (1)小车受重力,支持力和拉力,小车与滑轮间的细绳与长木板平行,测力计的示数等于小车所受的合外力;
(2)小车从靠近甲光电门处由静止开始做匀加速运动,位移x=$\frac{1}{2}$at2.位移一定,找出a与t的关系;
(3)根据牛顿第二定律求出小车的加速度和合力的关系,进一步求出F和$\frac{1}{{t}^{2}}$的关系式.
解答 解:(1)小车受重力,支持力和拉力,小车与滑轮间的细绳与长木板平行,测力计的示数等于小车所受的合外力,不需要满足沙和沙桶的总质量远小于小车的质量;
(2)小车从靠近甲光电门处由静止开始做匀加速运动,位移x=$\frac{1}{2}$at2.
改变小车质量m,测得多组M、t的值,所以加速度a=$\frac{2x}{{t}^{2}}$,位移不变,所以a与t2成反比,合外力一定时,加速度与质量成反比例”的图线是C.
(3)小车由静止开始做匀加速运动,位移L=$\frac{1}{2}$at2.a=$\frac{2L}{{t}^{2}}$
根据牛顿第二定律,对于沙和沙桶有:F合=F-mg=ma
F=$\frac{m•2L}{{t}^{2}}$则图线的斜率为:k=2mL=0.54kg•m
k与摩擦力是否存在无关,若小车与长木板间的摩擦不能忽略,如图3所示测得图线斜率将不变.
故答案为:(1)小车与滑轮间的细绳与长木板平行;不需要;(2)C;(3)0.54kg•m;不变.
点评 对于实验问题一定要明确实验原理,并且亲自动手实验,掌握匀变速直线运动的规律应用,熟练应用所学基本规律解决实验问题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
15. 物体从距地面高h处沿不同的支持面滑至地面,如图所示,a为光滑斜面,凸为粗糙斜面,c为粗糙曲面,物体的质量为m,在这三种过程中( )
物体从距地面高h处沿不同的支持面滑至地面,如图所示,a为光滑斜面,凸为粗糙斜面,c为粗糙曲面,物体的质量为m,在这三种过程中( )
 物体从距地面高h处沿不同的支持面滑至地面,如图所示,a为光滑斜面,凸为粗糙斜面,c为粗糙曲面,物体的质量为m,在这三种过程中( )
物体从距地面高h处沿不同的支持面滑至地面,如图所示,a为光滑斜面,凸为粗糙斜面,c为粗糙曲面,物体的质量为m,在这三种过程中( )| A. | 重力做功相同 | B. | 沿c下滑时重力做功最大 | ||
| C. | 重力势能的变化相同 | D. | 沿c下滑时重力势能的变化量最大 |
4.在“探究加速度与力、质量的关系”实验中为了研究加速度跟力和质量的关系,应该采用的研究实验方法是( )
| A. | 控制变量法 | B. | 假设法 | C. | 理想实验法 | D. | 图象法 |
14.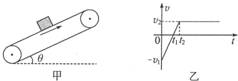 已知一足够长的传送带与水平面的倾角为θ,以恒定的速度顺时针转动.某时刻在传送带适当的位置放上具有一定初速度质量为m的小物块,如图甲所示.以此时为t=0时刻,小物块的速度随时间的变化关系如图乙所示(甲图中取沿传送带向上的方向为正方向,乙图中v1>v2),则下列判断正确的是( )
已知一足够长的传送带与水平面的倾角为θ,以恒定的速度顺时针转动.某时刻在传送带适当的位置放上具有一定初速度质量为m的小物块,如图甲所示.以此时为t=0时刻,小物块的速度随时间的变化关系如图乙所示(甲图中取沿传送带向上的方向为正方向,乙图中v1>v2),则下列判断正确的是( )
 已知一足够长的传送带与水平面的倾角为θ,以恒定的速度顺时针转动.某时刻在传送带适当的位置放上具有一定初速度质量为m的小物块,如图甲所示.以此时为t=0时刻,小物块的速度随时间的变化关系如图乙所示(甲图中取沿传送带向上的方向为正方向,乙图中v1>v2),则下列判断正确的是( )
已知一足够长的传送带与水平面的倾角为θ,以恒定的速度顺时针转动.某时刻在传送带适当的位置放上具有一定初速度质量为m的小物块,如图甲所示.以此时为t=0时刻,小物块的速度随时间的变化关系如图乙所示(甲图中取沿传送带向上的方向为正方向,乙图中v1>v2),则下列判断正确的是( )| A. | 0~t1内传送带对小物块做正功 | |
| B. | 小物块与传送带间的动摩擦因数μ>tanθ | |
| C. | 0~t2内传送带对小物块做功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv12 | |
| D. | 0~t2内小物块对传送带间因摩擦数产生的热量大于小物块动能的减少量 |
1.下列说法中正确的是( )
| A. | 直流电不能通过电感器 | |
| B. | 电感器对交流电没有阻碍 | |
| C. | 交流电的频率越高,电感器对电流的阻碍越明显 | |
| D. | 以上说法都不对 |
19.中国南车集团研制的“和谐号”380A新一代高速动车组最高时速达486.1公里,最高速度为486.1km/h,子弹以600m/s的速度从枪口射出,则( )
| A. | 486.1km/h是指平均速度,600m/s是指瞬时速度 | |
| B. | 486.1km/h和600m/s都是指平均速度 | |
| C. | 486.1km/h是指瞬时速度,600m/s是指平均速度 | |
| D. | 486.1km/h和600m/s都是指瞬时速度 |



 如图所示,A、B两辆车相距 s=11m,A车以vA=4m/s的速度向右匀速运动,而B车此时的速度vB=10m/s,向右以加速度2m/s2刹车,那么A车追上B车所用的时间为9s.
如图所示,A、B两辆车相距 s=11m,A车以vA=4m/s的速度向右匀速运动,而B车此时的速度vB=10m/s,向右以加速度2m/s2刹车,那么A车追上B车所用的时间为9s.