题目内容
【题目】如图所示, 光滑的水平地面上有一质量m = 1.0 kg的木板, 其右端放有一质量M = 2.0 kg的滑块, 左方有一竖直墙, 滑块与木板间的动摩擦因数μ = 0.2. 开始时, 木板与滑块以共同的速度v0 = 3.0 m/s向左运动, 某时刻木板与墙发生弹性碰撞, 碰撞时间极短. 已知木板足够长, 滑块始终在木板上, 重力加速度g = 10 m/s2. 求:
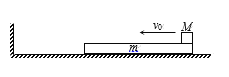
(1) 木板第一次与墙碰后再次与滑块速度相同时, 两者的共同速度;
(2) 木板第一次与墙碰后再次与滑块速度相同时, 木板左端到竖直墙的距离;
(3) 木板从第一次与墙碰撞到第二次碰撞所经历的时间.
【答案】 (1) v = 1.0 m/s ;(2) x = 1.0 m ;(3)t = 2.0 s
【解析】(1) 取向左为正方向, 设木板第一次与墙碰撞后再次与滑块共速时的速度为v, 由动量守恒定律有: Mv0 – mv0 = (M + m)v 解得: v =![]() = 1.0 m/s 方向向左
= 1.0 m/s 方向向左
(2) 对木板从第一次碰撞至再次与滑块速度相同的过程应用动能定理:
![]()
解得: ![]()
即木板第一次与墙碰后再次与滑块速度相同时, 木板左端到竖直墙的距离为1.0 m.
(3) 对木板从第一次碰撞至再次与滑块速度相同的过程应用动量定理:
![]() 解得:
解得: ![]()
之后木板和滑块一起匀速至第二次碰撞的时间: ![]()
故木板从第一次与墙碰撞到第二次碰撞所经历的时间: ![]()
综上所述本题答案是: (1) v = 1.0 m/s ;(2) x = 1.0 m ;(3)t = 2.0 s

【题目】如图所示,t=0时,质量为0.5 kg的物体从光滑斜面上的A点由静止开始下滑,经过B点进入水平面(设经过B点前后速度大小不变),最后停在C点,每隔2 s物体的瞬时速度记录在下表中,重力加速度g=10 m/s2,则下列说法中正确的是()
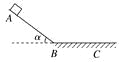
t/s | 0 | 2 | 4 | 6 |
v/(m·s-1) | 0 | 8 | 12 | 8 |
A.t=3 s时刻物体恰好经过B点
B.t=10 s时刻物体恰好停在C点
C.物体运动过程中的最大速度为12 m/s
D.A、B间的距离小于B、C间的距离