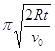��Ŀ����
����Ŀ����ͼ��ʾ���ᵯ�ɵ�һ�˹̶�����һ��������Ϊm�Ļ���B������B��ֹ��ˮƽ�����ϣ����ɴ���ԭ��״̬����һ������B��ͬ����A���ӵ����ϵ�P���Գ��ٶ�v0��B���У���A����l1�ľ���ʱ����B��������ײʱ�伫�̣�����A��B������һ���˶���������ճ������֪���Aǡ�÷��س�����P��ֹͣ������A��B�Կɿ����ʵ㣬�һ���A��B�뵼��Ļ���Ħ��������Ϊ�����˶������е�������α���Ϊl2����

��1��A��P����ʱ�ij��ٶ�v0
��2������ѹ�����ʱ�����ɵĵ��������Ƕ��٣�
���𰸡���1��![]() .��2��2��mg(L1+L2)
.��2��2��mg(L1+L2)
����������A�սӴ�Bʱ�ٶ�Ϊ![]() ������˲�乲ͬ�ٶ���
������˲�乲ͬ�ٶ���![]() �����ɽ�AB����������ԭ��ʱ���߹�ͬ�ٶ���
�����ɽ�AB����������ԭ��ʱ���߹�ͬ�ٶ���![]() ������ѹ�����ʱ���ɵĵ���������
������ѹ�����ʱ���ɵĵ���������![]()
��AΪ�о�����A����l1�Ĺ��̣��ɹ��ܹ�ϵ�ã� ![]()
��ABΪ�о�������ײ˲�����ɶ����غ�ã� ![]()
AB����ѹ�����ɵ�����α���Ϊl2�Ĺ��̣��ɹ��ܹ�ϵ�ã� ![]()
���ɽ�AB����������ԭ��λ�ù��̣��ɹ��ܹ�ϵ��![]()
�˺�AB���룬Aǡ�÷��س�����P��ֹͣ����A����һ���̣��ɹ��ܹ�ϵ��![]()
������ã� ![]()
![]()

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ