Question

【题目】在竖直平面内建立如图所示的平面直角坐标系．将一细杆的OM部分弯成抛物线形状，其抛物线部分的方程，细杆的MN部分为直线并与抛物线部分在M点相切；将弯好的细杆的O端固定在坐标原点且与x轴相切，与平面直角坐标系共面，M点的纵坐标yM＝0.8 m；一根处于原长(小于MN的长度)的轻弹簧套在MN上，下端固定在N点．现将一质量m＝0.1 kg的小球(中间有孔)套在细杆上，从O点以初速度v0＝5 m/s水平抛出，到达M点时速度vM＝6 m/s，小球继续沿杆下滑压缩弹簧到最低点C(图中未画出)，然后又被弹簧反弹，恰好能到达M点．已知小球与细杆间的动摩擦因数，sin 37°＝0.6，cos 37°＝0.8，空气阻力忽略不计．

(1)求抛出的小球在细杆的OM部分滑动时损失的机械能；

(2)求上述过程中弹簧的最大弹性势能；

(3)为使抛出的小球在细杆的OM部分滑运动时没有机械能损失，求小球从O点水平抛出时的初速度大小．

Answer 1

【答案】(1)0.25 J (2)8.1 J (3)3 m/s

【解析】

(1)根据动能定理有

代入已知条件得ΔE＝－Wf＝0.25 J．

(2)设由M点运动到最低点的距离为L，由动能定理有

其中θ为MN杆的倾角且

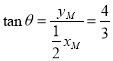
代入数据解得Ep＝8.1 J．

(3)小球与杆无压力时机械能损失最小，根据平抛运动规律有

代入数据解得v0＝3 m/s．