题目内容
13.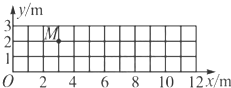 如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s.不计空气阻力,到达最高点的位置如图中M点所示(正方形,取g=10m/s2).求:
如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平.设平面内存在沿x轴正方向的恒定风力.一物体从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s.不计空气阻力,到达最高点的位置如图中M点所示(正方形,取g=10m/s2).求:(1)小球在M点的速度v1.
(2)在图中定性画出小球的运动轨迹并计算小球落回x轴时的位置N的坐标.
分析 (1)根据运动的分解,结合运动学公式,即可求解;
(2)根据竖直方向的对称性,结合水平方向做初速度为零的匀加速直线运动,从而即可求解.
解答 解:(1)设正方形的边长为s0.
竖直方向做竖直上抛运动,v0=gt1,2s0=$\frac{{v}_{0}}{2}$t1
水平方向做匀加速直线运动,有:3s0=$\frac{{v}_{1}}{2}$t1.
解得:v1=6 m/s.
(2)由竖直方向的对称性可知,小球再经过t1到x轴,水平方向做初速度为零的匀加速直线运动,所以回到x轴时落到x=12m处,位置N的坐标为(12,0).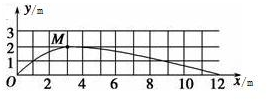
答:(1)小球在M点的速度6 m/s.
(2)如上图所示.
点评 考查运动学公式,掌握运动的合成与分解的应用,注意竖直上抛的对称性,理解牛顿第二定律的应用.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
3.为纪念邓小平诞辰110周年,2014年8月22日晚广安思源广场焰火晚会精彩上演.在形成焰火的烟花运动的过程中,以下说法中正确的是( )
| A. | 烟花的速度变化越快,加速度一定越大 | |
| B. | 烟花的速度越大,加速度也一定越大 | |
| C. | 烟花的加速度不断减小,速度一定越来越小 | |
| D. | 烟花的速度变化越大,加速度也一定越大 |
4. 如图所示,两个$\frac{1}{4}$圆弧形轨道竖直固定,相切于最低点P,⊙O2的半径是⊙O1半径R的两倍,圆心O1、O2与P点在同一竖直线上,以速率v1、v2水平抛出a、b两个质量相同的小球(均为质点),两小球恰好在P点相遇.若a、b两小球落在P点时的速度方向与竖直方向的夹角分别为α、β,重力加速度为g,则下列判断正确的是( )
如图所示,两个$\frac{1}{4}$圆弧形轨道竖直固定,相切于最低点P,⊙O2的半径是⊙O1半径R的两倍,圆心O1、O2与P点在同一竖直线上,以速率v1、v2水平抛出a、b两个质量相同的小球(均为质点),两小球恰好在P点相遇.若a、b两小球落在P点时的速度方向与竖直方向的夹角分别为α、β,重力加速度为g,则下列判断正确的是( )
 如图所示,两个$\frac{1}{4}$圆弧形轨道竖直固定,相切于最低点P,⊙O2的半径是⊙O1半径R的两倍,圆心O1、O2与P点在同一竖直线上,以速率v1、v2水平抛出a、b两个质量相同的小球(均为质点),两小球恰好在P点相遇.若a、b两小球落在P点时的速度方向与竖直方向的夹角分别为α、β,重力加速度为g,则下列判断正确的是( )
如图所示,两个$\frac{1}{4}$圆弧形轨道竖直固定,相切于最低点P,⊙O2的半径是⊙O1半径R的两倍,圆心O1、O2与P点在同一竖直线上,以速率v1、v2水平抛出a、b两个质量相同的小球(均为质点),两小球恰好在P点相遇.若a、b两小球落在P点时的速度方向与竖直方向的夹角分别为α、β,重力加速度为g,则下列判断正确的是( )| A. | v2=$\sqrt{2}$v1 | |
| B. | b球比a球先抛出的时间为$\sqrt{\frac{2R}{g}}$ | |
| C. | tanα=tanβ | |
| D. | b球落在P点时重力的瞬时功率是a球落在P点时重力的瞬时功率的2倍 |
1.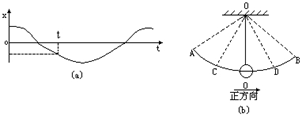 图(a)为单摆的振动图象,图(b)为单摆简谐运动的实际振动图示,则(b)图中t时刻摆球所在的位置为( )
图(a)为单摆的振动图象,图(b)为单摆简谐运动的实际振动图示,则(b)图中t时刻摆球所在的位置为( )
 图(a)为单摆的振动图象,图(b)为单摆简谐运动的实际振动图示,则(b)图中t时刻摆球所在的位置为( )
图(a)为单摆的振动图象,图(b)为单摆简谐运动的实际振动图示,则(b)图中t时刻摆球所在的位置为( )| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
8.一定量气体体积缩小外界做功40J,同时对外放热100J,气体内能的增量△U是( )
| A. | -60J | B. | 60J | C. | -140J | D. | 140J |
18.长10cm的导线,放入匀强磁场中,它的方向和磁场方向垂直,导线中的电流强度是3.0A,受到的磁场力是1.5×10-3N,则该处的磁感应强度B大小为( )
| A. | 5.0×10-3T | B. | 5.0×10-2T | C. | 5.0×10-1T | D. | 5.0T |
3. 一物理探究小组探究弹簧的伸长量与弹力的关系,所用装置如图,将弹簧和毫米刻度尺(最小分度值为1.0mm)竖直悬挂在铁架台上,依次在弹簧下端悬挂一个、两个、三个…钩码,已知每个钩码质量为50克.用刻度尺分别测量弹簧在挂个数不同钩码时的总长.取g=9.8N/kg.得到如下数据:
一物理探究小组探究弹簧的伸长量与弹力的关系,所用装置如图,将弹簧和毫米刻度尺(最小分度值为1.0mm)竖直悬挂在铁架台上,依次在弹簧下端悬挂一个、两个、三个…钩码,已知每个钩码质量为50克.用刻度尺分别测量弹簧在挂个数不同钩码时的总长.取g=9.8N/kg.得到如下数据:
①表格中有两个数据不符合读数规则,请把它们摘录下来填到横线上122.50、127.40:
②该弹簧的劲度系数为96N/m.
③该弹簧的原长为107.0mm,若将该弹簧放在水平面上测其原长,得到的结果比所填值小(填大或小).
 一物理探究小组探究弹簧的伸长量与弹力的关系,所用装置如图,将弹簧和毫米刻度尺(最小分度值为1.0mm)竖直悬挂在铁架台上,依次在弹簧下端悬挂一个、两个、三个…钩码,已知每个钩码质量为50克.用刻度尺分别测量弹簧在挂个数不同钩码时的总长.取g=9.8N/kg.得到如下数据:
一物理探究小组探究弹簧的伸长量与弹力的关系,所用装置如图,将弹簧和毫米刻度尺(最小分度值为1.0mm)竖直悬挂在铁架台上,依次在弹簧下端悬挂一个、两个、三个…钩码,已知每个钩码质量为50克.用刻度尺分别测量弹簧在挂个数不同钩码时的总长.取g=9.8N/kg.得到如下数据:| 钩码个数 | 1 | 2 | 3 | 4 |
| 弹簧总长(单位:mm) | 112.7 | 117.6 | 122.50 | 127.40 |
②该弹簧的劲度系数为96N/m.
③该弹簧的原长为107.0mm,若将该弹簧放在水平面上测其原长,得到的结果比所填值小(填大或小).
 如图,一滑块通过长度不计的短绳栓在小车的壁板上,小车表面光滑.小车由静止开始向右匀加速运动,经过2s,细绳断裂.细绳断裂后,小车的加速度不变,又经过一段时间,滑块从小车左端掉下,在这段时间内,已知滑块相对小车前3s内滑行了4.5m,后3s内滑行了10.5m.求:
如图,一滑块通过长度不计的短绳栓在小车的壁板上,小车表面光滑.小车由静止开始向右匀加速运动,经过2s,细绳断裂.细绳断裂后,小车的加速度不变,又经过一段时间,滑块从小车左端掉下,在这段时间内,已知滑块相对小车前3s内滑行了4.5m,后3s内滑行了10.5m.求: