��Ŀ����
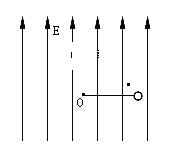
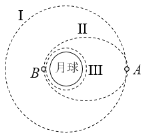
����Ŀ����ͼ��ʾ���������ھ��������߶�Ϊ3R��Բ�ι�������˶���������A�����������Բ����������������µ�B�ٴε�������¹��������������Բ���˶�����������뾶ΪR�����������������ٶ�Ϊg����
A. ��������B�㴦����������
B. ����֪����������������ڹ�����ϵ���������Ϊ5��![]()
C. ��������������������£��������ڹ������ͨ��B��ļ��ٶȴ����ڹ������ͨ��B��ļ��ٶ�
D. �������ڹ����������������һ�������ʱ��Ϊ2��![]()
���𰸡�BD
��������
��������棬�������������������������������������ṩ���������������̼�����⣬
���DZ��Ҳ���ǽ����˶��������˶��������ṩ�������������������������ϵȷ���ٶȹ�ϵ��
�ɴ��ڽ��¹�������������У������ṩ���������������������ڹ�ʽ������⣬�ڸ��ݿ����յ���������������ϵ�������
������ʲô����ϣ�ֻҪ��ͬһ���㣬�����ض���ͬ�����ٶȱض���ͬ��
A����Բ���ʵʩ������Բ���Զ�ص��������Բ�����쵽Բ�ι������������Բ�ĵ��˶���Ҫʵ������˶����������������ڷɴ�����������������Ӧ���ɴ������٣���С��������������ʵ����ܼ�С����A������
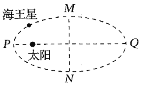
B����ɴ��ڽ��¹��������������һ�������ʱ��Ϊ![]() ����
����![]() ����ã�
����ã�![]() �����ݼ��ι�ϵ��֪�������İ볤��
�����ݼ��ι�ϵ��֪�������İ볤��![]() �����ݿ����յ�������
�����ݿ����յ�������![]() ������Եõ���
������Եõ���![]() ����BD��ȷ��
����BD��ȷ��
C��ֻ���������������£��������ڹ������ͨ��B��ļ��ٶȴ����ڹ������B��ľ�����ȣ�����������ͬ������ٶȹ���ȣ���C����