题目内容
【题目】（20分）如图所示，M、N为水平放置的平行金属板，板长和板间距均为2d。在金属板左侧板间中点处有电子源S，能水平发射初速为V0的电子，电子的质量为m，电荷量为e。金属板右侧有两个磁感应强度大小始终相等，方向分别垂直于纸面向外和向里的匀强磁场区域，两磁场的宽 度均为d。磁场边界与水平金属板垂直，左边界紧靠金属板右侧，距磁场右边界d处有一个荧光屏。过电子源S作荧光屏的垂线，垂足为O。以O为原点，竖直向下为正方向，建立y轴。现在M、N两板间加上图示电压，使电子沿SO方向射入板间后，恰好能够从金属板右侧边缘射出．进入磁场。（不考虑电子重力和阻力）
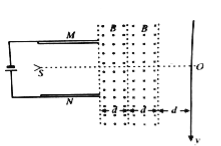
（1）电子进入磁场时的速度v；
（2）改变磁感应强度B的大小，使电子能打到荧光屏上，求
①磁场的磁感应强度大小的范围；
②电子打到荧光屏上位置坐标的范围。
【答案】（1）
；方向右下与水平方向的夹角为45°；（2）①
；②
到
。
【解析】
试题分析：（1）电子在MN间只受电场力作用，从金属板的右侧下边沿射出，有
（1分）
（1分）
（1分）
（1分）
解得 （1分）
速度偏向角
（1分）
（1分）
（2）电子恰能（或恰不能）打在荧光屏上，有磁感应强度的临界值
，此时电子在磁场中作圆周运动的半径为R
（2分）
又有
（2分）
由⑦⑧解得：
（1分）
磁感应强度越大，电子越不能穿出磁场，所以取磁感应强度时电子能打在荧光屏上（得
不扣分）。 （1分）
如图所示，电子在磁感应强度为时，打在荧光屏的最高处，由对称性可知，电子在磁场右侧的出射时速度方向与进入磁场的方向相同，
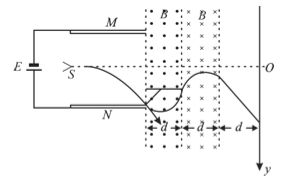
即。 （1分）
出射点位置到SO连线的垂直距离
（1分）
电子移开磁场后做匀速直线运动，则电子打在荧光屏的位置坐标
（1分）
解得
（1分）
当磁场的磁感应强度为零时，电子离开电场后做直线运动，打在荧光屏的最低点，其坐标为
（1分）
电子穿出磁场后打在荧光民屏上的位置坐标范围为：
到 （2分）
