题目内容
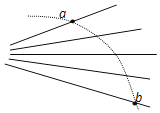
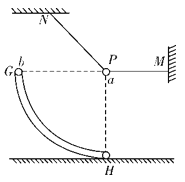
【题目】如图所示,带电小球a由绝缘细线PM和PN悬挂而处于静止状态,其中PM水平,地面上固定一绝缘且内壁光滑的圆弧细管道GH,圆心P与a球位置重合,管道底端H与水平地面相切,一质量为m可视为质点的带电小球b从G端口由静止释放,当小球b运动到H端时对管道壁恰好无压力,重力加速度为g。在小球b由G滑到H过程中,下列说法中正确的是
A. 细线PM的拉力先增大后减小
B. 小球b机械能逐渐减小
C. 小球b所受库仑力大小始终为2mg
D. 小球b加速度大小先变大后变小
【答案】A
【解析】
A. 设PN与竖直方向成α角,对球a受力分析,
竖直方向上有:FPNcosα=mg+F库sinθ
水平方向上有:F库cosθ+FPNsinα=FPM。
解得:FPM=mgtanα+3mgcos(θα)cosα,下滑时θ从0增大90°,细线PM的拉力先增大后减小,故A正确;
B. 在小球b由G滑到H过程中,小球b所受库仑力和管道的弹力始终与速度垂直,只有重力做功,库仑力和弹力不做功,小球b机械能守恒,故B错误;
C. 根据机械能守恒定律,小球b从G滑到H过程中,有:mgR=![]() ,
,
H处有:F库mg=![]() ,则有:F库=3mg,故C错误;
,则有:F库=3mg,故C错误;
D. 设b与a的连线与水平方向成θ角,则有:mgRsinθ=![]() ,任意位置加速度为向心加速度和切向加速度合成,
,任意位置加速度为向心加速度和切向加速度合成,
即为:a=![]() =
=![]() =
=![]() ,可知小球的加速度一直变大,故D错误。
,可知小球的加速度一直变大,故D错误。
故选:A。

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目