题目内容
【题目】如图所示，双星系统中的星球A、B都可视为质点，A、B绕两者连线上的O点做匀速圆周运动，A、B之间距离不变，引力常量为G，观测到A的速率为v、运行周期为T，二者质量分别为m1、m2．
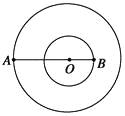
（1）求B的周期和速率．
（2）A受B的引力FA可等效为位于O点处质量为m′的星体对它的引力，试求m′．（用m1、m2表示）
【答案】（1）T；
（2）
【解析】试题分析：（1）双星是稳定的结构，故公转周期相同，故B的周期也为T．设A、B的圆轨道半径分别为r1、r2，由题意知，A、B做匀速圆周运动的角速度相同，其为ω．由牛顿运动定律：
对A：FA=m1ω2r1
对B：FB=m2ω2r2FA=FB
设A、B之间的距离为r，又r=r1+r2，由上述各式得：
，
故
（其中vA=v）
解得：
（2）A、B之间的距离r＝r1＋r2＝
r1，根据万有引力定律有
，
所以．
练习册系列答案
相关题目
