题目内容
【题目】如图,水平桌面固定着光滑斜槽,光滑斜糟的末端和一水平木板平滑连接,设物块通过衔接处时速率没有改变。质量m1=0.60kg的物块A从斜槽上端距水平木板高度h=0.80m处下滑,并与放在水平木板左端的质量m2=0.30kg的物块B相碰,相碰后物块B滑行x=4.0m到木板的C点停止运动。已知物块B与木板间的动摩擦因数μ=0.20,重力加速度g=10m/s2,求:(答案保留两位有效数字)
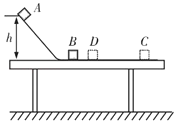
(1)物块A沿斜槽滑下与物块B碰撞前瞬间的速度大小
(2)滑动摩擦力对物块B做的功
(3)物块A与物块B碰撞过程中损失的机被能。
【答案】(1)4m/s(2)﹣2.4J(3)1.2J
【解析】
(1)设物块A滑到斜面底端与物块B碰撞前时的速度大小为v0,A在斜面上下滑过程,由机械能守恒定律得:![]()
解得:![]()
(2)设物块B受到的滑动摩擦力大小为f,摩擦力做功为W,则有:![]()
解得:![]()
(3)设物块A与物块B碰撞后瞬间的速度为v1,物块B碰撞后的速度为v,碰撞损失的机械能为E。对碰后B的运动过程,由动能定理得:![]()
解得:![]()
由动量守恒定律得:![]()
解得:![]()
由能量守恒得:![]()
解得:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目