题目内容
2.2004年,我国正式开展月球探测工程,并命名为“嫦娥工程”.嫦娥工程分为“无人月球探测”、“载人登月”和“建立月球基地”三个阶段,设想在月球表面上,宇航员登测出小物块自由下落h高度所用的时间为t,当飞船在靠近月球表面绕月球做匀速圆周运动时,测得其周期为T,已知引力常量为G,根据上述各量,试求:(1)月球表面的重力加速度g月;
(2)月球的质量M.
分析 (1)根据自由落体运动求月球表面的重力加速度;
(2)根据万有引力提供圆周运动向心力由近月卫星的周期与引力常量求月球的质量.
解答 解:(1)根据自由落体有:h=$\frac{1}{2}$g月t2
得月球表面的重力加速度为:g月=$\frac{2h}{{t}^{2}}$
(2)令月球半径为R,则月球表面重力万有引力相等,而近月飞行的卫星由万有引力提供向心力有:
mg月=G$\frac{Mm}{{R}^{2}}$=mR$\frac{4{π}^{2}}{{T}^{2}}$
解得月球半径为:
R=$\frac{{g}_{月}}{4{π}^{2}}$T2=$\frac{h{T}^{2}}{2{π}^{2}{t}^{2}}$
由根据重力与万有引力相等有:
G$\frac{mM}{{R}^{2}}$=mg月
月球的质量为:
M=$\frac{{g}_{月}{R}^{2}}{G}$=$\frac{2h}{G{t}^{2}}$•$\frac{{h}^{2}{T}^{4}}{4{π}^{4}{t}^{4}}$=$\frac{{h}^{3}{T}^{4}}{2G{π}^{4}{t}^{6}}$
答:(1)月球表面的重力加速度g月为$\frac{2h}{{t}^{2}}$;
(2)月球的质量M为$\frac{{h}^{3}{T}^{4}}{2G{π}^{4}{t}^{6}}$.
点评 解决本题的关键掌握万有引力提供向心力和万有引力等于重力这两个理论,并能灵活运用.本题重点是利用好月球表面的自由落体运动,这种以在星球表面自由落体、平抛物体、竖直上抛物体求解星球表面重力加速度的方式是比较常见的.

练习册系列答案
相关题目
7.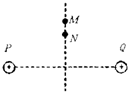 如图所示,空间存在两个等量同种的正的电荷P、Q,在P、Q连线的垂直平分线上有M、N两点,另有一点电荷q,则( )
如图所示,空间存在两个等量同种的正的电荷P、Q,在P、Q连线的垂直平分线上有M、N两点,另有一点电荷q,则( )
 如图所示,空间存在两个等量同种的正的电荷P、Q,在P、Q连线的垂直平分线上有M、N两点,另有一点电荷q,则( )
如图所示,空间存在两个等量同种的正的电荷P、Q,在P、Q连线的垂直平分线上有M、N两点,另有一点电荷q,则( )| A. | 若q是正电荷,q在N点的电势能比在M点的电势能大 | |
| B. | 若q是正电荷,由静止释放q电荷,则q在由N点向M运动时加速度在减小 | |
| C. | N点的场强比M点的场强大 | |
| D. | N点的电势比M点的电势高 |
11. 2013年我国相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球为R,月面的重力加速度为g月.以月面为零势能面.“玉兔”在h高度的引力势能可表示为EP=G$\frac{Mmh}{R(R+h)}$,其中G为引力常量,M为月球质量,若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
2013年我国相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球为R,月面的重力加速度为g月.以月面为零势能面.“玉兔”在h高度的引力势能可表示为EP=G$\frac{Mmh}{R(R+h)}$,其中G为引力常量,M为月球质量,若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
 2013年我国相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球为R,月面的重力加速度为g月.以月面为零势能面.“玉兔”在h高度的引力势能可表示为EP=G$\frac{Mmh}{R(R+h)}$,其中G为引力常量,M为月球质量,若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
2013年我国相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球为R,月面的重力加速度为g月.以月面为零势能面.“玉兔”在h高度的引力势能可表示为EP=G$\frac{Mmh}{R(R+h)}$,其中G为引力常量,M为月球质量,若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )| A. | $\frac{m{g}_{月}R}{R+h}$(h+2R) | B. | $\frac{m{g}_{月}R}{R+h}$(h+$\frac{1}{2}$R) | C. | $\frac{m{g}_{月}R}{R+h}$(h+$\frac{\sqrt{2}}{2}$R) | D. | $\frac{m{g}_{月}R}{R+h}$(h+$\sqrt{2}$) |

 如图所示,是物体向东做匀变速直线运动得到的一条纸带,从O点开始每5个计时点取一个计数点,依照打点的先后顺序依次编为1、2、3、4、5、6,测得相邻计数点之间的距离分别为s1=5.20cm,S2=4.42cm,s3=3.64cm,s4=2.80cm,s5=2.02cm,s6=1.24cm.
如图所示,是物体向东做匀变速直线运动得到的一条纸带,从O点开始每5个计时点取一个计数点,依照打点的先后顺序依次编为1、2、3、4、5、6,测得相邻计数点之间的距离分别为s1=5.20cm,S2=4.42cm,s3=3.64cm,s4=2.80cm,s5=2.02cm,s6=1.24cm.
 如图所示,两根平行且足够长的竖直金属导轨CD和EF间,横跨一根金属杆MN,MN可在导轨上无摩擦地上下滑动.磁感应强度为0.5T的水平匀强磁场垂直导轨所在平面.电池的电动势为1.5V,内阻不计,除MN有电阻外,其余部分电阻也不计.单刀双掷开关接通1-2时,MN棒恰好静止.若迅速把开关接通1-3,那么在MN下落过程中,1秒内扫过的最大面积为3m2.
如图所示,两根平行且足够长的竖直金属导轨CD和EF间,横跨一根金属杆MN,MN可在导轨上无摩擦地上下滑动.磁感应强度为0.5T的水平匀强磁场垂直导轨所在平面.电池的电动势为1.5V,内阻不计,除MN有电阻外,其余部分电阻也不计.单刀双掷开关接通1-2时,MN棒恰好静止.若迅速把开关接通1-3,那么在MN下落过程中,1秒内扫过的最大面积为3m2.