题目内容
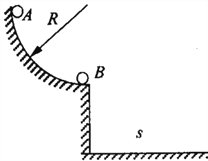
【题目】如图所示,一个半径为R=1.00m的![]() 粗糙圆孤轨道,固定在竖直平面内,其下端切线是水平的,轨道下端距地面高度为h=1.25m在轨道末端放有质量为mB=0.05kg的小球(视为质点),B左侧轨道下装有微型传感器,另一质量为mA=0.10kg的小球A(也视为质点)由轨道上端点从静止开始释放,运动到轨道最低处时,传感器显示读数为2.6N,A与B发生正碰,碰后B小球水平飞出,落到地面时的水平位移为s=1.00m,不计空气阻力,重力加速度取g=10m/s2.求:
粗糙圆孤轨道,固定在竖直平面内,其下端切线是水平的,轨道下端距地面高度为h=1.25m在轨道末端放有质量为mB=0.05kg的小球(视为质点),B左侧轨道下装有微型传感器,另一质量为mA=0.10kg的小球A(也视为质点)由轨道上端点从静止开始释放,运动到轨道最低处时,传感器显示读数为2.6N,A与B发生正碰,碰后B小球水平飞出,落到地面时的水平位移为s=1.00m,不计空气阻力,重力加速度取g=10m/s2.求:
(1)小球A运动到轨道最低处时的速度大小
(2)小球A在碰前克服摩擦力所做的功;
(3)A与B碰撞过程中,系统损失的机械能.
【答案】(1)4.00m/s(2)0.20J(3)0.25J
【解析】(1)在最低点对球由牛顿第二定律有:FA-mAg=![]()
解得vA=4.00m/s
(2)由动能定理有:mAgR-Wf=![]()
解得:Wf=0.20J
(3)碰后对B球平抛有: ![]()
![]()
∴v′B=2.0m/s
B碰由动量守恒定律有:mAvA=mAv′A+mBv′B
∴v′A=3.0m/s
由能量守恒得:ΔE损=![]()
故 ΔE损=0.25J

练习册系列答案
相关题目