题目内容
18. 如图所示,边界PQ以上和MN以下空间存在垂直纸面向里的匀强磁场,磁感应强度均为4B,PQ、MN间距离为2$\sqrt{3}$d,绝缘板EF、GH厚度不计,间距为d,板长略小于PQ、MN间距离,EF、GH之间有垂直纸面向里的匀强磁场,磁感应强度为B.有一个质量为m的带正电的粒子,电量为q,从EF的中点S射出,速度与水平方向成30°角,直接到达PQ边界并垂直于边界射入上部场区,轨迹如图所示,以后的运动过程中与绝缘板相碰时无能量损失且遵循反射定律,经过一段时间后该粒子能再回到S点.(粒子重力不计)求:①粒子从S点出发的初速度v;
如图所示,边界PQ以上和MN以下空间存在垂直纸面向里的匀强磁场,磁感应强度均为4B,PQ、MN间距离为2$\sqrt{3}$d,绝缘板EF、GH厚度不计,间距为d,板长略小于PQ、MN间距离,EF、GH之间有垂直纸面向里的匀强磁场,磁感应强度为B.有一个质量为m的带正电的粒子,电量为q,从EF的中点S射出,速度与水平方向成30°角,直接到达PQ边界并垂直于边界射入上部场区,轨迹如图所示,以后的运动过程中与绝缘板相碰时无能量损失且遵循反射定律,经过一段时间后该粒子能再回到S点.(粒子重力不计)求:①粒子从S点出发的初速度v; ②粒子从S点出发第一次再回到S点的时间;
③若其他条件均不变,EF板不动,将GH板从原位置起向右平移,且保证EFGH区域内始终存在垂直纸面向里的匀强磁场B,若仍需让粒子回到S点(回到S点的运动过程中与板只碰撞一次),则GH到EF的垂直距离x应满足什么关系?(用d来表示x)
分析 ①根据几何关系求出粒子在EF和GH间做圆周运动的轨道半径,结合半径公式求出粒子从S点出发的初速度.
②作出粒子运动的轨迹图,根据粒子在磁场中运动的周期公式,结合圆心角的大小求出粒子从S点出发第一次再回到S点的时间.
③作出粒子的轨迹图,结合粒子在磁场中运动的周期性,结合数学知识求出GH到EF的垂直距离x应满足通项表达式.
解答 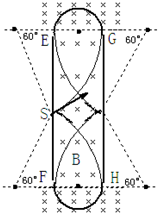 解:①粒子运动轨迹如图所示,
解:①粒子运动轨迹如图所示,
PQ、MN间的距离:L=2$\sqrt{3}$d,且s为中点,
由几何知识可知:R1sin60°=$\sqrt{3}$d,解得:R1=2d,
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{{R}_{1}}$,解得:v=$\frac{2qBd}{m}$;
②粒子运动轨迹如图所示,粒子应从G点进入PQ的场
在4B场内,由牛顿第二定律得:qv•4B=m$\frac{{v}^{2}}{{R}_{2}}$,解得:R2=$\frac{{R}_{1}}{4}$=$\frac{d}{2}$,
做半圆,并垂直PQ再由E点回到B场区,
由对称性,粒子将打到GH中点并反弹,再次回到S点的轨迹如图
粒子在B场中时间:t1=4×$\frac{1}{6}$T1=$\frac{2}{3}$×$\frac{2πm}{qB}$=$\frac{4πm}{3qB}$,
粒子在4B场中时间:t2=2×$\frac{1}{2}$T2=T2=$\frac{2πm}{q×4B}$=$\frac{πm}{2qB}$,
粒子的运动时间:t总=t1+t2=$\frac{11πm}{6qB}$;
③如图所示,由粒子运行的周期性以及与板碰撞遵循反射定律,有如下结果:
x=(3n+1)d (n=0、1、2…)或 x=3nd (n=0、1、2…);
答:①粒子从S点出发的初速度为$\frac{2qBd}{m}$;
②粒子从S点出发第一次再回到S点的时间为$\frac{11πm}{6qB}$;
③GH到EF的垂直距离x应满足x=(3n+1)d,(n=0,1,2,3…) 或 x=3nd,(n=0,1,2,3…).
点评 本题考查了带电粒子在磁场中的运动,关键作出轨迹图,结合半径公式、周期公式进行求解,在第三问中,要注意粒子运动的周期性.本题难度较大.

| A. | 直线电流的磁场,只分布在垂直于导线的某一个平面上 | |
| B. | 直线电流的磁感线是一些同心圆,磁感线的疏密是均匀的 | |
| C. | 通电直螺线管的磁感线分布与条形磁铁相同,在管内无磁场 | |
| D. | 通电长直螺线管的内部中间区域的磁感线是平等距直线 |
电压表(量程l5V,内阻约30kΩ); 电流表(量程300μA,内约50Ω);滑动变阻器(10Ω,1A);电池组(电动势E=12V,内阻r=6Ω);单刀单掷开关一个、导线若干.如表是他测量通过管中导电液柱的电流及两端电压的实验数据.实验中他还用游标卡尺测量了玻璃管的内径,结果如图2所示
| U/V | 0 | 1.0 | 3.0 | 5.0 | 7.0 | 9.0 | 11.0 |
| I/μA | 0 | 22 | 65 | 109 | 155 | 175 | 240 |

根据以上所述请回答下面的问题:
(1)玻璃管内径d的测量值为30.75cm;
(2)根据表1数据在坐标中描点做好图3,根据图象求出电阻R=4.6×104Ω(保留两位有效数字);
(3)计算导电溶液的电阻率表达式是ρ=$\frac{πR{d}^{2}}{4L}$ (用R、d、L表示);
(4)请在(图l)中补画出未连接的导线.
| A. | 阻力只与雨滴的半径成正比,即F=kr(k为常数) | |
| B. | 阻力只与雨滴的半径平方成正比,即F=kr2(k为常数) | |
| C. | 阻力只与速度的平方成正比,即F=kv2(k为常数) | |
| D. | 阻力与速度的平方和半径的乘积成正比,即F=krv2(k为常数) |
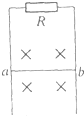 如图所示,匀强磁场和竖直导轨所在面垂直,金属棒ab可在导轨上无摩擦滑动,在金属棒、导轨和电阻组成的闭合回路中,除电阻R外,其余电阻均不计,在ab下滑过程中( )
如图所示,匀强磁场和竖直导轨所在面垂直,金属棒ab可在导轨上无摩擦滑动,在金属棒、导轨和电阻组成的闭合回路中,除电阻R外,其余电阻均不计,在ab下滑过程中( )| A. | 由于ab下落时有安培力做功,所以机械能不守恒 | |
| B. | ab达到稳定速度前,其减少的重力势能全部转化为电阻R的内能 | |
| C. | ab达到稳定速度后,其减少的重力势能全部转化为电阻R的内能 | |
| D. | ab达到稳定速度后,安培力不再对ab做功 |
| A. | 位移 | B. | 位移的增量 | C. | 加速度 | D. | 动能的增量 |
| A. | 9m/s | B. | 18m/s | C. | 10m/s | D. | 12m/s |
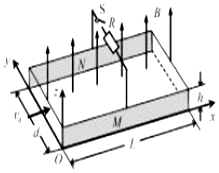 如图所示,某一新型发电装置的发电管是横截面为矩形的水平管道,管道的长为L、宽为d、高为h,上下两面是绝缘板.前后两侧面M、N是电阻可忽略的导体板,两导体板与开关S和定值电阻R相连.整个管道置于磁感应强度大小为B、方向沿z轴正方向的匀强磁场中.管道内始终充满电阻率为ρ的导电液体(有大量的正、负离子),且开关闭合前后,液体在管道进、出口两端压强差的作用下,均以恒定速率v0沿x轴正向流动,液体所受的摩擦阻力不变.
如图所示,某一新型发电装置的发电管是横截面为矩形的水平管道,管道的长为L、宽为d、高为h,上下两面是绝缘板.前后两侧面M、N是电阻可忽略的导体板,两导体板与开关S和定值电阻R相连.整个管道置于磁感应强度大小为B、方向沿z轴正方向的匀强磁场中.管道内始终充满电阻率为ρ的导电液体(有大量的正、负离子),且开关闭合前后,液体在管道进、出口两端压强差的作用下,均以恒定速率v0沿x轴正向流动,液体所受的摩擦阻力不变.