Question

【题目】如图所示，粗糙斜面的倾角θ=37°，边长L1=0.5 m的正方形区域内存在着垂直于斜面向下的匀强磁场。一个匝数n=10匝的刚性正方形线框，边长为L2=0.6 m，通过松弛的柔软导线（对线框的作用力近似为零）与电阻R相连，R=1.25 Ω。正方形磁场区域的一半恰好在正方形线框内部。已知线框质量m=2 kg，总电阻R0=1.25 Ω，与斜面间的动摩擦因数μ=0.5．从t=0时起，磁场的磁感应强度按B=B0－2t（T）的规律变化，线框能保持一段时间静止在斜面上。设最大静摩擦力等于滑动摩擦力，g取10m/s2，sin37°=0.6，cos37°=0.8．求：

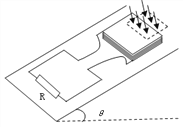
（1）线框不动时，回路中的感应电动势E；

（2）B0的取值范围；

（3）线框保持不动的时间内，电阻R上产生的热量Q的最大值是多少？

Answer 1

【答案】（1）2．5V（2）0．8T<B0≤4T（3）2J

【解析】

（1）

解得：E=2.5V

（2）

解得：I=1A

经分析可知：t=0时刻线圈若恰要上滑时有：

解得B0=4T

t=0时线圈若恰要下滑有：

解得B0=0．8T

则：0.8T<B0≤4T

（3）线框保持不动的最长时间为t，这段时间内磁感应强度从4T减小为0．8T

B=B0-2t

解得：t=1.6s

由Q=I2Rt

解得：Q=2J