题目内容
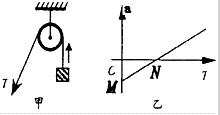 如图甲所示,某人通过动滑轮将质量为m的货物提升到一定高处,动滑轮的质量和摩擦均不计,货物获得的加速度a与竖直向上的拉力T之间的函数关系如图乙所示,则下列判断正确的是( )
如图甲所示,某人通过动滑轮将质量为m的货物提升到一定高处,动滑轮的质量和摩擦均不计,货物获得的加速度a与竖直向上的拉力T之间的函数关系如图乙所示,则下列判断正确的是( )| A、图线与纵轴的交点M的值aM=-g | ||
B、图线与横轴的交点N的值TN=
| ||
| C、图线的斜率等于物体的质量m | ||
D、D图线的斜率等于物体质量的倒数
|
分析:对货物受力分析,受重力和拉力,根据牛顿第二定律求出加速度的一般表达式进行分析.
解答:解:对货物受力分析,受重力mg和拉力T,根据牛顿第二定律,有:
T-mg=ma
解得:
a=
-g
A、当T=0时,a=-g,即图线与纵轴的交点M的值aM=-g,故A正确;
B、当a=0时,T=mg,故图线与横轴的交点N的值TN=mg,故B错误;
C、D、图线的斜率表示质量的倒数
,故C错误,D正确;
故选:AD.
T-mg=ma
解得:
a=
| T |
| m |
A、当T=0时,a=-g,即图线与纵轴的交点M的值aM=-g,故A正确;
B、当a=0时,T=mg,故图线与横轴的交点N的值TN=mg,故B错误;
C、D、图线的斜率表示质量的倒数
| 1 |
| m |
故选:AD.
点评:本题关键是根据牛顿第二定律求出加速度的一般表达式后对照a-T图象进行讨论.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 如图甲所示,某人正通过定滑轮将质量为m的货物提升到高处,滑轮的质量和摩擦均不计,货物获得的加速度a与绳子对货物竖直向上的拉力T之间的函数关系如图乙所示.g表示当地的重力加速度大小,由图可以判断( )
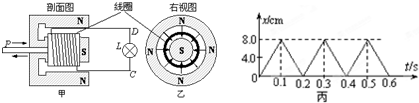
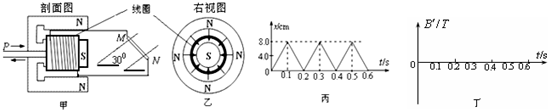
如图甲所示,某人正通过定滑轮将质量为m的货物提升到高处,滑轮的质量和摩擦均不计,货物获得的加速度a与绳子对货物竖直向上的拉力T之间的函数关系如图乙所示.g表示当地的重力加速度大小,由图可以判断( ) (2011?上海二模)如图甲所示是某人设计的一种振动发电装置,它的结构是一个套在辐向形永久磁铁槽中的半径为r=0.1m、匝数n=20的线圈,磁场的磁感线均沿半径方向均匀分布(其右视图如图乙所示).在线圈所在位置磁感应强度B的大小均为0.2T,线圈的电阻为2Ω,它的引出线接有8Ω的小电珠L.外力推动线圈框架的P端,使线圈沿轴线做往复运动,便有电流通过电珠.当线圈向右的位移x随时间t变化的规律如图丙所示时(x取向右为正),求:
(2011?上海二模)如图甲所示是某人设计的一种振动发电装置,它的结构是一个套在辐向形永久磁铁槽中的半径为r=0.1m、匝数n=20的线圈,磁场的磁感线均沿半径方向均匀分布(其右视图如图乙所示).在线圈所在位置磁感应强度B的大小均为0.2T,线圈的电阻为2Ω,它的引出线接有8Ω的小电珠L.外力推动线圈框架的P端,使线圈沿轴线做往复运动,便有电流通过电珠.当线圈向右的位移x随时间t变化的规律如图丙所示时(x取向右为正),求: