题目内容
(15分)如图所示,质量M=10kg、上表面光滑的足够长木板在F=50N的水平拉力作用下以v0=5m/s初速度沿水平地面向右匀速运动,现有足够多的小铁块,它们质量均为m=1kg,将一铁块无初速地放在木板最右端,当木板运动了L=1m时,又无初速地在木板最右端放上第二个铁块,只要木板运动了L就在木板最右端无初速地放一铁块。求:(g=10m/s2)

⑴第一个铁块放上后,木板运动1m时,木板的速度多大?
⑵最终能有几个铁块留在木板上?
⑶最后一个铁块与木板右端距离多大?

⑴第一个铁块放上后,木板运动1m时,木板的速度多大?
⑵最终能有几个铁块留在木板上?
⑶最后一个铁块与木板右端距离多大?
⑴v1=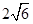 m/s;⑵n=7;⑶d=
m/s;⑵n=7;⑶d=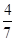 m
m
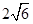 m/s;⑵n=7;⑶d=
m/s;⑵n=7;⑶d=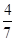 m
m试题分析:⑴开始时对木板受水平拉力F、重力Mg、地面的支持力N和滑动摩擦力f作用,设木板与地面间的动摩擦因数为μ,根据共点力平衡条件有:F=μMg ①
当第一个铁块放上后,木板将做匀减速直线运动,设木板运动1m时,木板的速度为v1,根据动能定理有:FL-μ(M+m)gL=
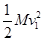 -
-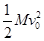 ②
②由①②式联立解得:v1=
 =
=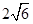 m/s,μ=
m/s,μ=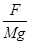 =0.5
=0.5⑵只要木板运动,就能有铁块增加,因此当木板速度减为零时,铁块不会再增加,设第n块铁块放上木板后,木板的速度减为零,即vn=0根据动能定理可知:
当第一块铁块放上木板时,有:FL-μ(M+m)gL=
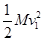 -
-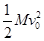
当第二块铁块放上木板时,有:FL-μ(M+2m)gL=
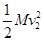 -
-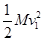
当第三块铁块放上木板时,有:FL-μ(M+3m)gL=
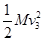 -
-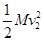
…
当第n块铁块放上木板时,有:FL-μ(M+nm)gL=
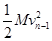 -0
-0累加以上各式,并联立①式得:
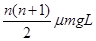 =
=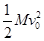 ,解得:n=6.6,取n=7
,解得:n=6.6,取n=7⑶设第7块铁块放上木板后离木板右端的距离为d,根据⑵中分析可知
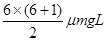 +μmgd=
+μmgd=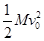
解得:d=
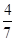 m
m
练习册系列答案
相关题目







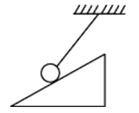
 的足够长固定光滑斜面底端有一与斜面垂直的挡板M,物块A、B之间用一与斜面平行的轻质弹簧连接且静止在斜面上。现用外力沿斜面向下缓慢推动物块B,当弹簧具有5J的弹性势能时撤去推力,释放物块B 。已知物块A、B的质量分别为5kg和10kg,弹簧的弹性势能的表达式为
的足够长固定光滑斜面底端有一与斜面垂直的挡板M,物块A、B之间用一与斜面平行的轻质弹簧连接且静止在斜面上。现用外力沿斜面向下缓慢推动物块B,当弹簧具有5J的弹性势能时撤去推力,释放物块B 。已知物块A、B的质量分别为5kg和10kg,弹簧的弹性势能的表达式为 ,其中弹簧的劲度系数为k=1000N/m,x为弹簧的形变量,g=10m/s2。求
,其中弹簧的劲度系数为k=1000N/m,x为弹簧的形变量,g=10m/s2。求
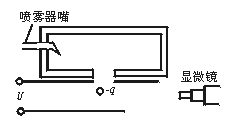
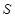 ,其活塞为梯形,它的一个面与气缸成
,其活塞为梯形,它的一个面与气缸成 角,活塞与器壁间的摩擦忽略不计,现用一水平力
角,活塞与器壁间的摩擦忽略不计,现用一水平力 推活塞,汽缸不动,此时大气压强为
推活塞,汽缸不动,此时大气压强为 ,求气缸内气体的压强
,求气缸内气体的压强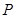 .
.
 处平衡;则A受到绳的拉力为( )
处平衡;则A受到绳的拉力为( )
