题目内容
【题目】两个中间有孔的质量为M的小球A、B用一轻弹簧相连,套在水平光滑横杆上。两个小球下面分别连一轻弹簧。两轻弹簧下端系在一质量为m的小球C上,如图所示。已知三根轻弹簧的劲度系数都为k,三根轻弹簧刚好构成一等边三角形。下列说法正确的是
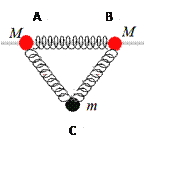
A. 水平横杆对质量为M的小球的支持力为Mg+mg
B. 连接质量为m小球的轻弹簧的弹力为mg/3
C. 连接质量为m小球的轻弹簧的伸长量为![]()
D. 套在水平光滑横杆上的轻弹簧的形变量![]()
【答案】C
【解析】A、选择整体为研究的对象,它们在竖直方向只受到重力与杆的支持力,由二力平衡可知,杆的支持力与整体的重力大小相等,即N=2Mg+mg,所以水平横杆对质量为M的小球的支持力为Mg+mg/2,故A错误;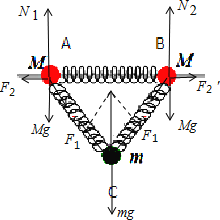
B、对三个小球分别进行受力分析如图:
则:由对称性可知,左右弹簧对C的拉力大小相等,与合力的方向之间的夹角30°,所以:2F1cos30°=mg
得:F1=![]() mg,故B错误;
mg,故B错误;
C、由胡克定律得:F1=kx1,连接质量为m小球的轻弹簧的伸长量: x1=F1/k=![]() ,故C正确;
,故C正确;
D、对A进行受力分析如图,则水平方向受到水平弹簧向左的弹力与F1的水平分力的作用,由受力平衡得:
F2=F1cos60= ![]()
同理,对B进行受力分析得:F′2=F1cos60= ![]() ,所以弹簧的弹力是
,所以弹簧的弹力是![]() ,套在水平光滑横杆上的轻弹簧的形变量:x′=F2/k=
,套在水平光滑横杆上的轻弹簧的形变量:x′=F2/k=![]() ,故D错误。
,故D错误。
故选:C。

练习册系列答案
相关题目