题目内容
19. 如图所示,两个劲度系数分别为k1和k2的轻质弹簧竖直悬挂,弹簧下端用光滑细绳连接,并有一光滑的轻滑轮放在细绳上,当滑轮下端挂一重为G的物体后,滑轮下滑一段距离,则下列结论正确的有( )
如图所示,两个劲度系数分别为k1和k2的轻质弹簧竖直悬挂,弹簧下端用光滑细绳连接,并有一光滑的轻滑轮放在细绳上,当滑轮下端挂一重为G的物体后,滑轮下滑一段距离,则下列结论正确的有( )| A. | 两弹簧的伸长量相等 | |
| B. | 两弹簧的弹力不相等 | |
| C. | 重物下降的距离为$\frac{G}{({k}_{1}+{k}_{2})}$ | |
| D. | 重物下降的距离为$\frac{G({k}_{1}+{k}_{2})}{4{k}_{1}{k}_{2}}$ |
分析 对滑轮进行受力分析,应用平衡条件可求得弹簧的弹力,重物下降的距离就是两根弹簧伸长的量除以2.
解答 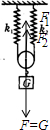 解:对滑轮受力分析如图:
解:对滑轮受力分析如图:
因为F1、F2是同一根绳上的力,故大小相等,即:F1=F2
由平衡条件得:F1+F2=G
解得:F1=$\frac{G}{2}$
由胡克定律公式F=kx得弹簧1伸长量为:
x1=$\frac{\frac{G}{2}}{{k}_{1}}$=$\frac{G}{2{k}_{1}}$
弹簧2伸长量为:
x2=$\frac{\frac{G}{2}}{{k}_{2}}$=$\frac{G}{2{k}_{2}}$
弹簧共伸长:
x=x1+x2=$\frac{G}{2{k}_{1}}$+$\frac{G}{2{k}_{2}}$=$\frac{G({k}_{1}+{k}_{2})}{{2k}_{1}{k}_{2}}$
重物下降的距离为:d=$\frac{x}{2}$=$\frac{G({k}_{1}+{k}_{2})}{{4k}_{1}{k}_{2}}$
故ABC错误,D正确;
故选:D.
点评 本题为受力平衡的简单应用,受力分析后应用平衡条件求解即可;注意应用动滑轮的基本原理.

练习册系列答案
相关题目
9.下列关于路程和位移的说法正确的是( )
| A. | 路程是矢量,位移是标量 | B. | 路程可以等于位移 | ||
| C. | 路程总大于位移的大小 | D. | 路程可以等于位移的大小 |
14.科学家在研究原子、原子核及基本粒子时,为了方便,常常用元电荷作为电量的单位,关于元电荷,下列论述中正确的是( )
| A. | 把质子或电子叫元电荷 | |
| B. | 1.6×10-19 C的电量叫元电荷 | |
| C. | 所有带电体的带电量一定等于元电荷的整数倍 | |
| D. | 元电荷的数值最早是由美国物理学家密立根用实验测得的 |
11.某导线中的电流是2A,通过导线横截面的电荷量为12C,所需要的时间为( )
| A. | 2s | B. | 6s | C. | 4s | D. | 8s |
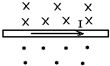
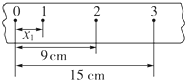 某同学做了一次较为精确的测定手拉纸带运动的加速度的实验,得到的纸带如图所示,设O点是计数的起始点(不是打点计时器打下的第一个点),两计数点之间的时间间隔为0.1s,x1=3cm,则打第二个计数点1时的瞬时速度约为0.45m/s,打第三个计数点2时的瞬时速度约为0.6m/s,手的加速度a=1.5 m/s2.
某同学做了一次较为精确的测定手拉纸带运动的加速度的实验,得到的纸带如图所示,设O点是计数的起始点(不是打点计时器打下的第一个点),两计数点之间的时间间隔为0.1s,x1=3cm,则打第二个计数点1时的瞬时速度约为0.45m/s,打第三个计数点2时的瞬时速度约为0.6m/s,手的加速度a=1.5 m/s2.