��Ŀ����
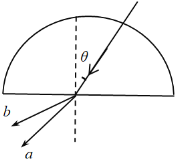
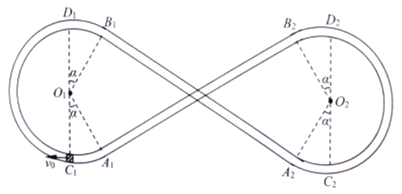
����Ŀ����ͼ��ʾ������ֱƽ������һ��![]() ���ܵ�װ�ã�������������ȫ��ͬ��Բ���ܵ�����ֱ�ܵ���ɡ�ֱ�ܵ���Բ���ܵ��ֱ�������
���ܵ�װ�ã�������������ȫ��ͬ��Բ���ܵ�����ֱ�ܵ���ɡ�ֱ�ܵ���Բ���ܵ��ֱ�������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ�����Բ���ܵ�����ߵ㣬
�ֱ�����Բ���ܵ�����ߵ㣬![]() ��
��![]() �ֱ�����Բ���ܵ�����͵㣬
�ֱ�����Բ���ܵ�����͵㣬![]() ��
��![]() �̶���ͬһˮƽ�����ϡ���ֱ�ܵ�������������Բ���ܵ��⻬��ֱ�ܵ��ֲڣ��ܵ��Ĵ�ϸ�ɺ��ԡ�Բ���ܵ��İ뾶��ΪR��
�̶���ͬһˮƽ�����ϡ���ֱ�ܵ�������������Բ���ܵ��⻬��ֱ�ܵ��ֲڣ��ܵ��Ĵ�ϸ�ɺ��ԡ�Բ���ܵ��İ뾶��ΪR��![]() ��һ����Ϊm��С�����ˮƽ������ٶ�
��һ����Ϊm��С�����ˮƽ������ٶ�![]() ��
��![]() ������عܵ��˶���С�����ֱ�ܵ���Ķ�Ħ������Ϊ
������عܵ��˶���С�����ֱ�ܵ���Ķ�Ħ������Ϊ![]() ����
����![]() ��m=1kg��R=1.5m��
��m=1kg��R=1.5m��![]() ��
��![]() ��sin37��=0.6��cos37��=0.8������
��sin37��=0.6��cos37��=0.8������
��1��С����![]() �����ʱ�Թܵ�����������
�����ʱ�Թܵ�����������
��2��С����һ�ξ���![]() ��ʱ���ٶȴ�С��
��ʱ���ٶȴ�С��
��3��С�����ֱ�ܵ�![]() �Ͼ�������·�̡�
�Ͼ�������·�̡�
���𰸡���1��106N���������£�2��4![]() m/s��3��
m/s��3��![]() m
m
��������
(1)�����C1����Բ���˶�����ţ�ٵڶ������У�
![]()
�ɵã�![]()
��ţ�ٵ������ɿ�֪��С���Թܵ�����������СΪ106N����������
(2)�ɼ���֪ʶ���У�![]()
��C1��C2�ɶ��ܶ����ɵã�![]()
�ɵã�![]()
(3)��C1C2ˮƽ����Ϊ�������ܵIJο�ƽ�棬��С���Խ��D1��D2��ʱ�Ļ�е�������㣺
![]()
����ֱ�ܵ���Ħ�������ÿ��������ֱ�ܵ�һ�Σ���е�ܵļ��������㣺
![]()
��nΪ�ӵ�һ�ξ���D1��ԽD1��D2���ܴ��������У�
![]() ��
��
![]()
�ɵã�n=2������С����ڵڶ��ξ���D1��͵�����D2��֮����D1B1A2C2D2֮�������˶�ֱ���ȶ��������A2��C2�Ҳ���A2�ȸߴ�֮�������ȶ��˶���
�ɿ�ʼ���ȶ��˶�����A2�㣬�ɶ��ܶ����У�
![]()
�ɵã�s=![]() m
m
����B1A2ֱ�ܵ��Ͼ�����·��Ϊs'=s��l=![]() m
m