Question

【题目】如图所示，光滑斜面倾角为θ，底端固定一垂直于斜面的挡板C．在斜面上放置长木板A，A的下端与C的距离为d，A的上端放置小物块B，A、B的质量均为m，A．B间的动摩擦因数μ＞tanθ．现同时由静止释放A、B，A与C发生碰撞的时间极短，碰撞前后瞬间速度大小相等，运动过程中小物块始终没有从木板上滑落，已知重力加速度为g求：

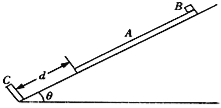
（l）A与C发生第一次碰撞前瞬间的速度大小v1；

（2）A与C发生第一次碰撞后上滑到最高点时，小物块B的速度大小V2；

（3）为使B不与C碰撞，木板A长度的最小值L．

Answer 1

【答案】（l）A与C发生第一次碰撞前瞬间的速度大小v1为．

（2）A与C发生第一次碰撞后上滑到最高点时，小物块B的速度大小V2为．

（3）为使B不与C碰撞，木板A长度的最小值L是4d．

【解析】解：（1）第一次碰撞前，由机械能守恒得

2m=2mgdsinθ

解得 v1=

（2）设发生第一次碰撞后，A上滑、B下滑的加速度大小分别为aA、aB，则

μmgcosθ+mgsinθ=maA；

μmgcosθ﹣mgsinθ=maB；

可知aA＞aB，则知A先减速到零，设A第一次碰撞后后上滑到最高点的时间为t，则

v1=aAt

v2=v1﹣aBt

联立解得 v2=

（3）研究A、B运动的全过程，由能量守恒定律有

mgdsinθ+mg（d+L）sinθ=μmgLcosθ

解得 L=4d

答：

（l）A与C发生第一次碰撞前瞬间的速度大小v1为．

（2）A与C发生第一次碰撞后上滑到最高点时，小物块B的速度大小V2为．

（3）为使B不与C碰撞，木板A长度的最小值L是4d．