题目内容
【题目】如图所示，质量为m的小球在细线A和轻弹簧B的共同作用下保持静止，其中细线A水平，左端固定于竖直墙壁，轻弹簧B上端固定于天花板，轴线与竖直方向的夹角为600，已知轻弹簧B的劲度系数为后，重力加速度为g，求：
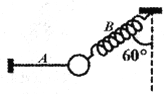
(1)细线A中拉力的大小FA；
(2)轻弹簧B的伸长量Δx；
(3)突然剪断细线A的瞬间，小球的加速度a．
【答案】（1）
（2）
（3）
【解析】试题分析：对小球受力分析，利用平衡条件即可求出细线A和轻弹簧B中的拉力，结合胡克定律求出轻弹簧B的伸长量；弹簧的弹力不能突变，则突然撤去外力的瞬间弹力不变，由牛顿第二定律即可求出加速度。
对小球受力分析如图所示：
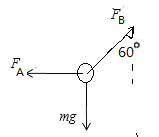
根据平衡条件，在水平方向上有： 
在竖直方向上有： 
联立以上解得： 
（2）由上可知
根据胡克定律： 
可得轻弹簧B的伸长量为： 
（3）弹簧的弹力不能突变，则突然撤去外力的瞬间弹力不变，仍有： 
由牛顿第二定律得： 
解得： 
水平向右
练习册系列答案
名校课堂系列答案
相关题目
