题目内容
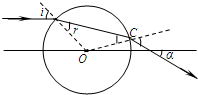
如图所示,MN是一条通过透明球体球心的直线.在真空中的单色细光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的
倍,且与MN所成的角α=30°.求:透明体的折射率.

| 2 |

连接OB、BC,如图所示.
在B点光线的入射角、折射角分别标为i、r,在△OCP中:有
| OC |
| sinα |
| OP |
| sin∠OCP |
解得∠OCP=135°(45°值舍)①
进而可得:∠COP=15°
由折射率定义:在B点有:n=
| sini |
| sinr |
在C点有:n=
| sin(180°-135°) |
| sin∠BCO |
又∠BCO=r
所以,i=45°②
又:∠BCO=180°-i-∠COP=120°故:r=30°③
因此,透明体的折射率n=
| sini |
| sinr |
| sin45° |
| sin30° |
| 2 |
答:透明体的折射率为
| 2 |

练习册系列答案
相关题目