题目内容
6.如图所示,宽为L=2m、足够长的金属导轨MN和M′N′放在倾角为θ=30°的斜面上,在N和N′之间连有一个阻值为R=1.2Ω的电阻,在导轨上AA′处放置一根与导轨垂直、质量为m=0.8kg、电阻为r=0.4Ω的金属滑杆,导轨的电阻不计.用轻绳通过定滑轮将电动小车与滑杆的中点相连,绳与滑杆的连线平行于斜面,开始时小车位于滑轮的正下方水平面上的P处(小车可视为质点),滑轮离小车的高度H=4.0m.在导轨的NN′和OO′所围的区域存在一个磁感应强度B=1.0T、方向垂直于斜面向上的匀强磁场,此区域内滑杆和导轨间的动摩擦因数为μ=$\frac{\sqrt{3}}{4}$,此区域外导轨是光滑的.电动小车沿PS方向以v=1.0m/s的速度匀速前进时,滑杆经d=1m的位移由AA’滑到OO’位置.(g取10m/s2)求: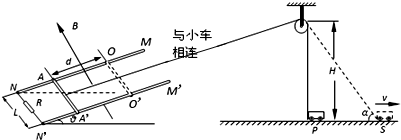
(1)请问滑杆AA′滑到OO′位置时的速度是多大?
(2)若滑杆滑到OO′位置时细绳中拉力为10.1N,滑杆通过OO′位置时的加速度?
(3)若滑杆运动到OO′位置时绳子突然断了,则从断绳到滑杆回到AA′位置过程中,电阻R上产生的热量Q为多少?(设导轨足够长,滑杆滑回到AA’时恰好做匀速直线运动.)
分析 (1)由速度公式求出金属棒通过cd时的速度大小v;
(2)感应电动势为E=BLv,由欧姆定律求出电流,由安培力公式求出安培力,然后由牛顿第二定律求出加速度.
(3)由平衡条件求出滑杆的速度,由能量守恒定律求出产生的热量.
解答 解:(1)滑杆运动到OO'位置时,小车通过S点时的速度为v=1.0m/s,
设系绳与水平面的夹角为α,则
滑杆$\frac{H}{sinα}$-H=d,sinα=0.8,α=53°
此时向上的速度即绳端沿绳长方向的速度,代入数据得:v1=0.6m/s.
(2)滑杆运动到OO'位置产生感应电动势为:E=BLv1,
产生感应电流为:I=$\frac{E}{R+r}$,
受到的安培力为:F安=BIL=$\frac{{B}^{2}{L}^{2}{v}_{1}}{R+r}$,代入数据,得:F安=1.5N.
滑杆通过OO'位置时所受摩擦力为:f=μmgcosθ=$\frac{\sqrt{3}}{4}$×0.8×10×$\frac{\sqrt{3}}{2}$=3N.
由F-mgsinθ-f-F安=ma,
解得加速度:a=2m/s2.
(3)设滑杆返回运动到AA'位置后做匀速运动的速度为v2,有:mgsinθ=μmgcosθ+$\frac{{B}^{2}{L}^{2}{v}_{2}}{R+r}$,
带入数据,可得:v2=0.4m/s
由功能关系:Q=$\frac{1}{2}$mv12-$\frac{1}{2}$mv22+mgdsinθ-μmgdcosθ,
带入数据得:Q=1.08J
所以,由串联电路特点可得:QR=$\frac{R}{R+r}•Q$=$\frac{1.2}{1.2+0.4}×1.08$=0.81J.
答:(1)滑杆AA′滑到OO′位置时的速度是0.60m/s;
(2)若滑杆滑到OO′位置时细绳中拉力为10.1N,滑杆通过OO′位置时的加速度是2m/s2;
(3)若滑杆运动到OO′位置时绳子突然断了,则从断绳到滑杆回到AA′位置过程中,电阻R上产生的热量Q为0.81J.
点评 本题是一道电磁感应与力学、电学相结合的综合体,考查了求加速度、电阻产生的热量,分析清楚滑杆的运动过程,应用运动的合成与分解、E=BLv、欧姆定律、安培力公式、牛顿第二定律、平衡条件、能量守恒定律即可正确解题;求R产生的热量时要注意,系统产生的总热量为R与r产生的热量之和.

 考前必练系列答案
考前必练系列答案| A. | 电场和电场线都是人为构想出来的,实际上不存在 | |
| B. | 同一电场中,电场线越密集的地方电场强度越大;越稀疏的地方电场越弱 | |
| C. | 在电场中,电场线通过的地方场强不为零,不画电场线的地方电场强度为零 | |
| D. | 电荷之间的相互作用是通过电场来完成的,场是一种物质 |
| A. | 1.875×106 | B. | 3.75×106 | C. | 1.875×105 | D. | 3.75×105 |
| A. | 滑动摩擦力的方向总是与物体的运动方向相反 | |
| B. | 滑动摩擦力总是阻碍物体的运动 | |
| C. | 滑动摩擦力的方向总是与物体的相对运动方向相反 | |
| D. | 两个互相接触且挤压的物体发生相对运动时,它们受到的滑动摩擦力方向相反 |
 一转动装置如图所示,四根长均为l的轻杆OA、OC,AB和CB,与两小球及一小环通过饺链连接,球和环的质量均为m,O端固定在竖直的轻质转轴上,套在轴上的轻质弹簧连接在O与小环之间,原长为L,裝置静止时,弹簧长为$\frac{3}{2}$L.己知弹簧始终在弹性限度内,忽略摩擦和空气阻力,则( )
一转动装置如图所示,四根长均为l的轻杆OA、OC,AB和CB,与两小球及一小环通过饺链连接,球和环的质量均为m,O端固定在竖直的轻质转轴上,套在轴上的轻质弹簧连接在O与小环之间,原长为L,裝置静止时,弹簧长为$\frac{3}{2}$L.己知弹簧始终在弹性限度内,忽略摩擦和空气阻力,则( )| A. | 弹簧的劲度系效为$\frac{2mg}{L}$ | |
| B. | 装置静止时,弹簧弹力等于mg | |
| C. | 转动该装置并缓慢增大转速,AB杆中弹力先减小后增大 | |
| D. | AB杆中弹力为零时,装置转动的角速度为$\sqrt{\frac{8g}{5L}}$ |
| A. | 两表指针偏角相同?? | |
| B. | 两表指针都不偏转 | |
| C. | 伏特表指针有偏转,安培表指针几乎不偏转 | |
| D. | 安培表指针有偏转,伏特表指针几乎不偏转 |
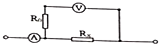 如图所示,一伏安法测电阻的电路中,电压表的量程为3V,内阻为1kΩ,测量时发现电压表的量程过小,在电压表上串联一个阻值为1kΩ的定值电阻R0,最后电压表示数为2.50V,电流表示数为0.10A,关于Rx下列说法正确的是( )
如图所示,一伏安法测电阻的电路中,电压表的量程为3V,内阻为1kΩ,测量时发现电压表的量程过小,在电压表上串联一个阻值为1kΩ的定值电阻R0,最后电压表示数为2.50V,电流表示数为0.10A,关于Rx下列说法正确的是( )| A. | Rx等于50Ω | B. | Rx大于50Ω | C. | Rx等于25Ω | D. | Rx小于25Ω |
 如图1所示,光滑水平桌面上,竖直木钣abcd紧靠在桌边后方,cd边水平,木板与桌边在同一个竖直平面内.一小球在桌面以速度v平行木板向右做匀速运动,经过ad边的前方时,木板开始做自由落体运动,则小球在木板上投影的轨道大致是图中的( )
如图1所示,光滑水平桌面上,竖直木钣abcd紧靠在桌边后方,cd边水平,木板与桌边在同一个竖直平面内.一小球在桌面以速度v平行木板向右做匀速运动,经过ad边的前方时,木板开始做自由落体运动,则小球在木板上投影的轨道大致是图中的( )