题目内容
18.同步卫星A距地面高度为h,近地卫星B距地面高度忽略不计,地球半径为R,地面上赤道处物体C相对于地面静止.则A、B、C三者角速度、向心加速度和线速度的比例关系为ωA:ωB:ωC=$\sqrt{{R}^{3}}$:$\sqrt{(R+h)^{3}}$:$\sqrt{{R}^{3}}$,,aA:aB:aC=R2(R+h):(R+h)3:R3,vA:vB:vC=$\sqrt{R}$(R+h):$\sqrt{(R+h)^{3}}$:$\sqrt{{R}^{3}}$.分析 人造地球卫星均由万有引力充当向心力,则有公式可求得加速度及线速度的表达式;从而得出比值;由于地球上赤道上的物体万有引力不是全部充当向心力,不能直接求比;只能根据同步卫星与地球的自转周期相同,由a=rω2和v=rw求出A与C的加速度及线速度的关系,再由AB间的关系得出AC间的关系
解答 解:卫星的向心力由万有引力提拱,则对AB两卫星,由万有引力公式可求得向心加速度及线速度、角速度之比;
故G$\frac{Mm}{{r}^{2}}$=ma=m$\frac{{v}^{2}}{r}$=mω2r
可得:
a=$\frac{GM}{{r}^{2}}$;v=$\sqrt{\frac{GM}{r}}$,ω=$\sqrt{\frac{GM}{{r}^{3}}}$
故同步卫星与近地卫星的加速度之比为:$\frac{{a}_{A}}{{a}_{B}}$=$\frac{{R}^{2}}{(R+h)^{2}}$;
线速度之比为:$\frac{{v}_{A}}{{v}_{B}}$=$\sqrt{\frac{R}{R+h}}$;
角速度之比为:$\frac{{ω}_{A}}{{ω}_{B}}$=$\sqrt{\frac{{R}^{3}}{(R+h)^{3}}}$
对于AC,因同步卫星的角速度与地球上的物体的角速度相同,故由a=ω2R,v=ωR,
可得$\frac{{a}_{A}}{{a}_{C}}$=$\frac{R+h}{R}$;$\frac{{v}_{A}}{{v}_{C}}$=$\frac{R+h}{R}$,$\frac{{ω}_{A}}{{ω}_{C}}$=$\frac{1}{1}$
综上知ωA:ωB:ωC=$\sqrt{{R}^{3}}$:$\sqrt{(R+h)^{3}}$:$\sqrt{{R}^{3}}$,aA:aB:aC=R2(R+h):(R+h)3:R3,vA:vB:vC=$\sqrt{R}$(R+h):$\sqrt{(R+h)^{3}}$:$\sqrt{{R}^{3}}$
故答案为:$\sqrt{{R}^{3}}$:$\sqrt{(R+h)^{3}}$:$\sqrt{{R}^{3}}$,R2(R+h):(R+h)3:R3,$\sqrt{R}$(R+h):$\sqrt{(R+h)^{3}}$:$\sqrt{{R}^{3}}$.
点评 本题应注意由于地球表面的物体其万有引力充当了重力和向心力,故地球表面的物体不能直接利用万有引力公式,而是利用圆周运动的相关公式进行分析求解.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案A.待测电阻器Rx(2.5V,1.2W) B.电流表A(0~0.6A,内阻为1Ω)
C.电压表V(0~3V,内阻未知) D.滑动变阻器(0~10Ω,额定电流1A)
E.电源(E=3V,内阻r=1Ω) F.定值电阻R0(阻值5Ω)
G.开关一个和导线若干
(1)实验时,该同学采用电流表内接法,并且电阻器两端电压从零开始变化,请在图1内画出实验电路图.
(2)按照正确的电路图,该同学测得实验数据如下(请补充完整):
| I/A | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.48 |
| U/V | 0.25 | 0.40 | 0.60 | 0.90 | 1.25 | 1.85 | 2.50 | 3.00 |
| UR/V | 0.10 | 0.20 | 0.60 | 0.90 | 2.05 | 2.52 |

(3)该同学将本实验中的电阻器Rx以及给定的定值电阻R0二者串联起来,接在本实验提供的电源两端,则电阻器的实际功率是0.32W.(结果保留2位小数)
 如图所示,P、Q为带等量负电荷的点电荷,O为其连线的中点,A、B为其中垂线上的两点,则下列说法中正确的是( )
如图所示,P、Q为带等量负电荷的点电荷,O为其连线的中点,A、B为其中垂线上的两点,则下列说法中正确的是( )| A. | 负电荷在A点的电势能大于在B点的电势能 | |
| B. | 正电荷在A点的电势能大于在B点的电势能 | |
| C. | A点的场强一定大于B点的场强 | |
| D. | 将带正电的试探电荷从A移动到B点过程中,电场力做正功 |
| A. | 增大 | B. | 减小 | ||
| C. | 不变 | D. | 由于两物体质量未知,无法确定 |
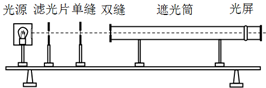 图示为双缝干涉的实验示意图,光源发出的光经滤光片成为单色光,然后通过单缝和双缝,在光屏上出现明暗相间的条纹.若要使干涉条纹的间距变大,在保证其他条件不变的情况下,可以( )
图示为双缝干涉的实验示意图,光源发出的光经滤光片成为单色光,然后通过单缝和双缝,在光屏上出现明暗相间的条纹.若要使干涉条纹的间距变大,在保证其他条件不变的情况下,可以( )| A. | 将光屏移近双缝 | |
| B. | 更换滤光片,改用波长更长的单色光 | |
| C. | 增大单缝与双缝的间距 | |
| D. | 将光源向双缝移动一小段距离 |
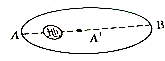 如图所示,一人造卫星绕地球作椭圆轨道运动,试比较该卫星在近地点与远地点时的重势能大小.
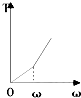
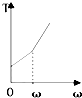
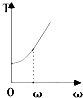
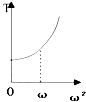
如图所示,一人造卫星绕地球作椭圆轨道运动,试比较该卫星在近地点与远地点时的重势能大小.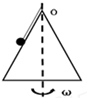 用一根细线一端系一可视为质点的小球,另一端固定在一光滑圆锥顶上,如右图所示,设小球在水平面内作匀速圆周运动的角速度为ω,线的张力为T,则T随ω2变化的图象是下图中的( )
用一根细线一端系一可视为质点的小球,另一端固定在一光滑圆锥顶上,如右图所示,设小球在水平面内作匀速圆周运动的角速度为ω,线的张力为T,则T随ω2变化的图象是下图中的( )