题目内容
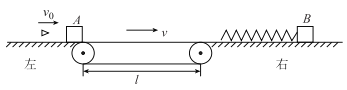
【题目】如图所示,光滑、足够长的两水平面中间平滑对接有一等高的水平传送带,质量m=0.9kg的小滑块A和质量M=4kg的小滑块B静止在水平面上,小滑块B的左侧固定有一轻质弹簧,且处于原长。传送带始终以v=1m/s的速率顺时针转动。现用质量m0=100g的子弹以速度v0=40m/s瞬间射入小滑块A,并留在小滑块A内,两者一起向右运动滑上传送带。已知小滑块A与传送带之间的动摩擦因数μ=0.1,传送带两端的距离l=3.5m,两小滑块均可视为质点,忽略空气阻力,重力加速度g=10m/s2。求:
(1)小滑块A滑上传送带左端时的速度大小
(2)小滑块A在第一次压缩弹簧过程中弹簧的最大弹性势能
(3)小滑块A第二次离开传送带时的速度大小
【答案】(1)4 m/s(2)3.6 J(3)1.0m/s
【解析】
(1)子弹打人小滑块A的过程中,动量守恒
![]()
解得
v1=4 m/s
(2)小滑块A从传送带的左端滑到右端的过程中,根据动能定理有
![]()
代人数据解得
v2=3 m/s
因为v2>v,所以小滑块A在第一次到达传送带右端时速度大小为3m/s,小滑块A第一次压编弹簧的过程中,当小滑块A和B的速度相等时,弹簧的弹性势能最大,根据动量守恒定律有
![]()
代人数据解得
v3=0.6m/s
根据能量守恒定律得
![]()
代人数据解得
Epm=3.6 J
(3)从小滑块A开始接触弹簧到弹簧恢复原长,整体可看成弹性碰撞,则有
![]()
![]()
解得
v4=-1.8 m/s
v3=1.2 m/s
设小滑块A又滑回传送带上且减速到零时在传送带上滑动的距离为L,则根据动能定理有
![]()
解得
L=1.62m
由于L<l,小滑块A滑回传送带上先减速到零,再在传送带上加速到与传送带共速,设小滑块A与传送带共速时向右滑动的距离为s,则根据运动学公式得
![]()
解得
s=0.5m
由于s<L,则小滑块A第二次从传送带离开时的速度大小为1.0m/s。且从传送带右端离开.