题目内容
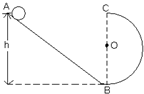 如图所示,一质量为m的小球自光滑斜面顶端A由静止开始自由滑下,在斜面底端B进入半径为R的光滑圆形轨道,已知小球在B处无能量损失,式求:
如图所示,一质量为m的小球自光滑斜面顶端A由静止开始自由滑下,在斜面底端B进入半径为R的光滑圆形轨道,已知小球在B处无能量损失,式求:(1)A点离轨道最底点至少多高时,小球就可以到达圆形轨道的最高点?
(2)此过程中,小球通过圆形轨道的最底点B时对轨道的压力有多大?
分析:(1)小球恰能到达最高点C点时,只受重力作用,用牛顿第二定律可得此位置的速度,由A到C的过程中机械能守恒,列式可得A点的高度
(2)由A到B的过程机械能守恒,可求出小球在B点的速度,再对小球受力分析,由牛顿第二定律可得轨道对小球的支持力,结合牛顿第三定律可得小球对轨道的压力.
(2)由A到B的过程机械能守恒,可求出小球在B点的速度,再对小球受力分析,由牛顿第二定律可得轨道对小球的支持力,结合牛顿第三定律可得小球对轨道的压力.
解答:解:(1)小球恰能到达圆形轨道的最高点C点时,重力提供向心力,由牛顿第二定律有:
mg=m
解得:vc=
小球由A到C的过程中,只有重力做功,机械能守恒,则有:
mgh=
m
+mg?2R
解得:h=
R
(2)小球由A到B的过程中,只有重力做功,机械能守恒,则有:
mgh=
m
解得:vB=
小球在B点时,受力分析,受竖直向下的重力和竖直向上的支持力,合力提供向心力,则由牛顿第二定律有:
FN-mg=m
解得:FN=6mg
由牛顿第三定律有:
=FN=6mg
答:(1)A点离轨道最底点至少多为
R时,小球就可以到达圆形轨道的最高点.
(2)此过程中,小球通过圆形轨道的最底点B时对轨道的压力为6mg.
mg=m
| ||
| R |
解得:vc=
| Rg |
小球由A到C的过程中,只有重力做功,机械能守恒,则有:
mgh=
| 1 |
| 2 |
| v | 2 c |
解得:h=
| 5 |
| 2 |
(2)小球由A到B的过程中,只有重力做功,机械能守恒,则有:
mgh=
| 1 |
| 2 |
| v | 2 B |
解得:vB=
| 5Rg |
小球在B点时,受力分析,受竖直向下的重力和竖直向上的支持力,合力提供向心力,则由牛顿第二定律有:
FN-mg=m
| ||
| R |
解得:FN=6mg
由牛顿第三定律有:
| F | ′ N |
答:(1)A点离轨道最底点至少多为
| 5 |
| 2 |
(2)此过程中,小球通过圆形轨道的最底点B时对轨道的压力为6mg.
点评:该题考查了机械能守恒,要熟练的掌握机械能守恒的条件以及重力做功的特点;此题的关键是向心力的确定,知道小球恰能通过圆形轨道最高点的条件是速度为v=
,小球运动到圆形轨道的最低点时,支持力和重力的合力提供向心力.若要求的是小球对轨道的压力,一定不要忘记牛顿第三定律.
| gR |

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 如图所示,一质量为m,带电荷量为+q的小物体,在水平方向的匀强磁场B中,从倾角为
如图所示,一质量为m,带电荷量为+q的小物体,在水平方向的匀强磁场B中,从倾角为 如图所示,一质量为m=0.016kg、长L=0.5m、宽d=0.1m、电阻R=0.1Ω的矩形线圈,从h1=5m的高处由静止开始下落,然后进入高度为h2(h2>L)的匀强磁场.下边刚进入磁场时,线圈正好作匀速运动.线圈的下边通过磁场所经历的时间t=0.15s.取g=10m/s2
如图所示,一质量为m=0.016kg、长L=0.5m、宽d=0.1m、电阻R=0.1Ω的矩形线圈,从h1=5m的高处由静止开始下落,然后进入高度为h2(h2>L)的匀强磁场.下边刚进入磁场时,线圈正好作匀速运动.线圈的下边通过磁场所经历的时间t=0.15s.取g=10m/s2 如图所示,一质量为m的物块恰好沿着倾角为θ的斜面匀速下滑.现对物块施加一个竖直向下的恒力F.则物块( )
如图所示,一质量为m的物块恰好沿着倾角为θ的斜面匀速下滑.现对物块施加一个竖直向下的恒力F.则物块( ) 如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平恒力F的作用下,从最低点A点拉至B点的过程中,力F所做的功为( )
如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平恒力F的作用下,从最低点A点拉至B点的过程中,力F所做的功为( ) 如图所示,一质量为m=1.0×10-2kg,带电量为q=1.0×10-6C的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成37°角.小球在运动过程电量保持不变,重力加速度g取10m/s2.
如图所示,一质量为m=1.0×10-2kg,带电量为q=1.0×10-6C的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成37°角.小球在运动过程电量保持不变,重力加速度g取10m/s2.