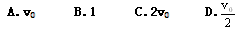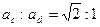题目内容
如图21所示，第四象限内有互相正交的匀强电场E与匀强磁场B1，E的大小为1.5×103V／m，Bl大小为0.5T；第一象限的某个矩形区域内，有方向垂直纸面的匀强磁场B2，磁场的下边界与x轴重合。一质量m=1×10-14kg、电荷量q=2×l0-10C的带正电微粒以某一速度v沿与y轴正方
向60°角
从M点沿直线运动，经P点即进入处于第一象限内的磁场B2区域。一段时间后，小球经过y轴上的N点并与y轴正方向成60°角的方向飞出。M点的坐标为（0，-10），N点的坐标为（0，30），不计粒子重力，g取10m/s2。则求：
（1）微粒运动速度v的大小；
（2）匀强磁场B2的大小；
（3）B2磁场区域的最小面积。
向60°角从M点沿直线运动，经P点即进入处于第一象限内的磁场B2区域。一段时间后，小球经过y轴上的N点并与y轴正方向成60°角的方向飞出。M点的坐标为（0，-10），N点的坐标为（0，30），不计粒子重力，g取10m/s2。则求：（1）微粒运动速度v的大小；
（2）匀强磁场B2的大小；
（3）B2磁场区域的最小面积。
（1）
。
（2）画出微粒的运动轨迹如图，粒子做圆周运动
的半径为
由
，解得
。
（3）由图可知，磁场B2的最小区域应该分布在图示的矩形PACD内，由几何关系易得
所以，所求磁场的最小面积为
。（2）画出微粒的运动轨迹如图，粒子做圆周运动
的半径为由
，解得。（3）由图可知，磁场B2的最小区域应该分布在图示的矩形PACD内，由几何关系易得
所以，所求磁场的最小面积为
略
练习册系列答案
相关题目
线框，总电阻为R.线框以垂直磁场边界的速度
匀速通过磁场区域.在运动过程中，线框ab、cd两边
始终与磁场边界平行.设线框刚进入磁场的位置x=0，x轴沿水平方向向右.求：
.（不需要分析说明）
（如图），求微粒的入射速度v2。
／B
。
介子回到P点所用时间。
