题目内容
5. 如图所示是推动节水工程的转动喷水“龙头”,“龙头”距地面高为h=1m,可将水水平喷出,其喷灌半径可达10h,每分钟喷水m=600kg,所用的水从地下H=3m深的井里抽取.设水以相同的速率水平喷出,水泵效率为η=80%.不计空气阻力,试求:
如图所示是推动节水工程的转动喷水“龙头”,“龙头”距地面高为h=1m,可将水水平喷出,其喷灌半径可达10h,每分钟喷水m=600kg,所用的水从地下H=3m深的井里抽取.设水以相同的速率水平喷出,水泵效率为η=80%.不计空气阻力,试求:(1)水从喷水“龙头”喷出的速率;
(2)水泵每分钟对水做的功;
(3)带动水泵的电动机的最小输出功率.
分析 (1)根据平抛运动的知识求出喷水龙头喷出水的初速度.
(2)水泵对水做的功转化为水的动能和重力势能,根据功能关系分析.
(3)带动水泵的电动机的最小输出功率等于水泵输入功率.
解答 解:(1)水平抛运动所用的时间 t=$\sqrt{\frac{2h}{g}}$
水平初速度为 v=$\frac{10h}{t}$=5$\sqrt{2gh}$=10$\sqrt{5}$ m/s.
(2)1 min内喷出水的动能为Ek=$\frac{1}{2}$mv2=25mgh=1.5×105 J.
水泵提水,1 min内水获得的重力势能为Ep=mg(H+h)=2.4×104 J.
1 min内水泵对水做的功 W=Ek+Ep=(1.5×105+2.4×104) J=1.74×105 J.
(3)带动水泵的电动机的最小输出功率等于水泵输入功率
P=$\frac{mg(H+26h)}{60η}$=3.6×103 W.
答:
(1)水从喷水“龙头”喷出的速率为10$\sqrt{5}$ m/s.
(2)水泵每分钟对水做的功为1.74×105 J.
(3)带动水泵的电动机的最小输出功率为3.6×103 W
点评 本题考查了平抛运动的规律,以及要熟练运用能量守恒定律分析能量是如何转化的.

练习册系列答案
相关题目
11.自由下落的物体,在任何相邻的单位时间内下落的距离之差△h和平均速度之差△$\overline{v}$在数值上分别等于( )
| A. | $\frac{g}{2}$ 2g | B. | $\frac{g}{2}$ $\frac{g}{4}$ | C. | g g | D. | g 2g |
12.一质点在x轴上运动,初速度v0>0,加速度a>0,则( )
| A. | 质点某一秒末的速度一定比前一秒末的速度大2a | |
| B. | 质点某一秒末的速度一定比前一秒初的速度大2a | |
| C. | 若a是变值,在a减小到零的过程中,速度的变化减小到零,末速度仍为V0 | |
| D. | 若a是变值,在a减小到零后,物体运动最快 |
17. 如图,以直角三角形AOC为边界的有界匀强磁场区域,磁场方向垂直于纸面向里,磁感应强度大小为B,∠A=60°,AO=a.在O点放置一个粒子源,可以向纸面内各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法不正确的是( )
如图,以直角三角形AOC为边界的有界匀强磁场区域,磁场方向垂直于纸面向里,磁感应强度大小为B,∠A=60°,AO=a.在O点放置一个粒子源,可以向纸面内各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法不正确的是( )
 如图,以直角三角形AOC为边界的有界匀强磁场区域,磁场方向垂直于纸面向里,磁感应强度大小为B,∠A=60°,AO=a.在O点放置一个粒子源,可以向纸面内各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法不正确的是( )
如图,以直角三角形AOC为边界的有界匀强磁场区域,磁场方向垂直于纸面向里,磁感应强度大小为B,∠A=60°,AO=a.在O点放置一个粒子源,可以向纸面内各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法不正确的是( )| A. | 粒子在磁场中运动的半径为a | |
| B. | 粒子有可能打到A点 | |
| C. | 以θ=60°飞入的粒子在磁场中运动时间最短 | |
| D. | 在AC边界上只有一半区域有粒子射出 |
14.两个大小一定的共点力F1和F2的合力为F,下列说法不正确的是( )
| A. | F一定大于任何一个分力 | |
| B. | F的大小可能等于F1,也可能等于F2 | |
| C. | 若把F分解,若知道两个分力的方向(与合力不共线),则只能作出唯一一个平行四边形 | |
| D. | F的大小随F1、F2间的夹角的增大而减小 |
15. 如图,两光滑的金属导轨之间存在一匀强磁场,方向垂直指向纸里.导轨的一端经导线与一灯泡A相接,另一端用导线闭合,一金属框置于导轨之上,框与灯泡B串联.当金属框按图示方向运动时( )
如图,两光滑的金属导轨之间存在一匀强磁场,方向垂直指向纸里.导轨的一端经导线与一灯泡A相接,另一端用导线闭合,一金属框置于导轨之上,框与灯泡B串联.当金属框按图示方向运动时( )
 如图,两光滑的金属导轨之间存在一匀强磁场,方向垂直指向纸里.导轨的一端经导线与一灯泡A相接,另一端用导线闭合,一金属框置于导轨之上,框与灯泡B串联.当金属框按图示方向运动时( )
如图,两光滑的金属导轨之间存在一匀强磁场,方向垂直指向纸里.导轨的一端经导线与一灯泡A相接,另一端用导线闭合,一金属框置于导轨之上,框与灯泡B串联.当金属框按图示方向运动时( )| A. | A、B两盏灯都不亮 | B. | A、B两盏灯都发亮 | C. | 灯泡A发亮,B不亮 | D. | 灯泡A不亮,B发亮 |
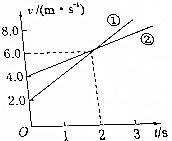 图中的直线①和②分别表示两个物体运动的速度图象,它们的初速度各是多大?哪一个的加速度大?经过多长时间它们的速度大小相等?
图中的直线①和②分别表示两个物体运动的速度图象,它们的初速度各是多大?哪一个的加速度大?经过多长时间它们的速度大小相等? 如图所示,一物体以6m/s的速度冲上一足够长的光滑斜面,物体在斜面上运动的加速度大小为2m/s2,经过多长时间物体的速度大小为2m/s(物体在斜面上运动的加速度恒定).
如图所示,一物体以6m/s的速度冲上一足够长的光滑斜面,物体在斜面上运动的加速度大小为2m/s2,经过多长时间物体的速度大小为2m/s(物体在斜面上运动的加速度恒定).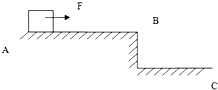 如图所示,用F=8N的水平拉力,使质量m=1kg的物体从A点由静止开始沿光滑水平桌面做匀加速直线运动,到达桌子边缘B点时撤掉力F,物体飞出桌面后落到地上C点,已知A、B之间的距离s=8m,桌面高H=1m,求:
如图所示,用F=8N的水平拉力,使质量m=1kg的物体从A点由静止开始沿光滑水平桌面做匀加速直线运动,到达桌子边缘B点时撤掉力F,物体飞出桌面后落到地上C点,已知A、B之间的距离s=8m,桌面高H=1m,求: