题目内容
12.发射火箭的时候,火箭中的物体会处于超重状态.已知一物体在地球表面重20N,它在以6m/s2的加速度竖直加速上升的火箭中的视重为17N,则此时火箭离地球表面的距离为地球半径的多少倍?(已知地球表面的重力加速度g=10m/s2)分析 对物体进行受力分析,由牛顿第二定律可以求出火箭所在位置处的重力加速度;由万有引力等于重力,列式可以求出火箭所在位置处的高度.
解答 解:设此时火箭所在处的重力加速度为g′,地球表面的重力加速度为g.
物体的质量为 m=$\frac{{G}_{\;}}{g}$=$\frac{20}{10}$=2kg,
对处在火箭中的物体,应用牛顿第二定律得:N-mg′=ma,
重力加速度:g′=2.5m/s2=$\frac{1}{4}$g,
在地表时,物体的重力等于地球对它的引力:mg=G$\frac{Mm}{{R}^{2}}$,
在高为h的位置上,有:mg′=G$\frac{Mm}{(R+h)^{2}}$,
解得:$\frac{g′}{g}$=$\frac{{R}^{2}}{(R+h)^{2}}$=$\frac{1}{4}$,解得:h=R;
此时火箭离地球表面的距离为地球半径的1倍.
答:此时火箭离地球表面的距离为地球半径的1倍.
点评 本题考查了万有引力定律的应用,本题解题的关键是:要知道重力等于万有引力,能熟练应用牛顿第二定律、万有引力定律公式即可正确解题.

练习册系列答案
相关题目
5.如图所示是P、Q两质点运动的位移-时间图象,由图可以判断( )
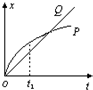

| A. | P质点的速度越来越大 | |
| B. | P开始时的速度较大 | |
| C. | 在P与Q的交叉点前,P质点的速度大于Q质点的速度 | |
| D. | 在P与Q的交叉点,两质点的速度相等 |
3.穿过闭合回路的磁通量随时间变化的图象分别如图①-④所示,下列关于回路中产生的感应电动势的论述,正确的是( )
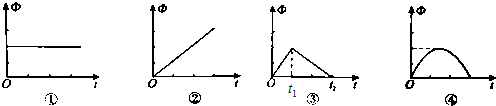

| A. | 图①中回路产生的感应电动势恒定不变 | |
| B. | 图②中回路产生的感应电动势一直在增大 | |
| C. | 图③中回路在0-t1内产生的感应电动势小于在t1-t2内产生的感应电动势 | |
| D. | 图④中回路产生的感应电动势先变小后变大 |
20.关于机械能守恒定律的适用条件,下列说法中正确的是( )
| A. | 对于单个物体,只有重力和弹力作用时,机械能守恒 | |
| B. | 当有其他外力作用时,只要合外力为零,机械能守恒 | |
| C. | 当有其他外力作用时,只要其他力的合力的功为零,机械能守恒 | |
| D. | 炮弹在空中飞行不计阻力时,仅受重力作用,所以爆炸前后机械能守恒 |
7.两个相同的金属小球,带电量之比为$\frac{1}{7}$,相距为r,两者相互接触后再放回原来的位置上,则它们的静电力可能为原来的( )
| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{9}{7}$ | D. | $\frac{16}{7}$ |
1.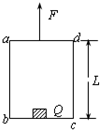 如图所示,在高为L的木箱abcd的底部放有一个小物体Q(可视为质点),现用力F向上拉绳,使木箱由静止开始运动,若保持拉力的功率不变,经过t时间,木箱达到最大速度,这时让木箱实然停止,小物体由于惯性会继续向上运动,且恰能达到木箱顶端.若重力加速度为g,空气阻力不计,以下说法正确的是( )
如图所示,在高为L的木箱abcd的底部放有一个小物体Q(可视为质点),现用力F向上拉绳,使木箱由静止开始运动,若保持拉力的功率不变,经过t时间,木箱达到最大速度,这时让木箱实然停止,小物体由于惯性会继续向上运动,且恰能达到木箱顶端.若重力加速度为g,空气阻力不计,以下说法正确的是( )
 如图所示,在高为L的木箱abcd的底部放有一个小物体Q(可视为质点),现用力F向上拉绳,使木箱由静止开始运动,若保持拉力的功率不变,经过t时间,木箱达到最大速度,这时让木箱实然停止,小物体由于惯性会继续向上运动,且恰能达到木箱顶端.若重力加速度为g,空气阻力不计,以下说法正确的是( )
如图所示,在高为L的木箱abcd的底部放有一个小物体Q(可视为质点),现用力F向上拉绳,使木箱由静止开始运动,若保持拉力的功率不变,经过t时间,木箱达到最大速度,这时让木箱实然停止,小物体由于惯性会继续向上运动,且恰能达到木箱顶端.若重力加速度为g,空气阻力不计,以下说法正确的是( )| A. | 木箱即将达到最大速度之前,物体Q处于超重状态 | |
| B. | 木箱突然停止运动时,物体Q处于超重状态 | |
| C. | 木箱的最大速度为$\sqrt{2gL}$ | |
| D. | 可以确定t时间内木箱上升的高度 |
19.有一个单摆,在竖直平面内做小摆角振动,周期为2s.如果从单摆向左运动通过平衡位置时开始计时,在t=1.4s至t=1.5s的过程中,摆球的( )
| A. | 速度向右在增大,加速度向右在减小 | |
| B. | 速度向左在增大,加速度向左也在增大 | |
| C. | 速度向左在减小,加速度向右在增大 | |
| D. | 速度向右在减小,加速度向左在增大 |
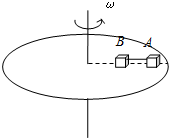 如图所示,在匀速转动的水平圆盘上,沿半径方向放置两个用细线相连的质量均为m的小物体A、B,它们到转轴的距离分别为rB=10cm,rA=50cm,A、B与盘间最大静摩擦力均为重力的k=0.3倍,g取10m/s2,试求:
如图所示,在匀速转动的水平圆盘上,沿半径方向放置两个用细线相连的质量均为m的小物体A、B,它们到转轴的距离分别为rB=10cm,rA=50cm,A、B与盘间最大静摩擦力均为重力的k=0.3倍,g取10m/s2,试求: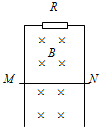 如图所示,MN为金属杆,在竖直平面内贴着光滑平行金属导轨下滑,导轨的间距l=10cm,导轨上端接有电阻R=0.5Ω,导轨与金属杆的电阻不计,整个装置处于B=0.5T的水平匀强磁场中,磁场方向垂直于导轨平面.当金属杆MN稳定下滑时,每秒钟有0.02J的重力势能转化为电能,求
如图所示,MN为金属杆,在竖直平面内贴着光滑平行金属导轨下滑,导轨的间距l=10cm,导轨上端接有电阻R=0.5Ω,导轨与金属杆的电阻不计,整个装置处于B=0.5T的水平匀强磁场中,磁场方向垂直于导轨平面.当金属杆MN稳定下滑时,每秒钟有0.02J的重力势能转化为电能,求