题目内容
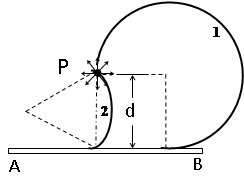
如图所示,在足够长的绝缘板上方距离为d的P点有一个粒子发射源,能够在纸面内向各个方向发射速率相等,比荷q/m=k的带正电的粒子,不考虑粒子间的相互作用和粒子重力。

(1)若已知粒子的发射速率为vo,在绝缘板上方加一电场强度大小为E、方向竖直向下的匀强电场,求同一时刻发射出的带电粒子打到板上的最大时间差;
(2)若已知粒子的发射速率为vo,在绝缘板的上方只加一方向垂直纸面,磁感应强度B= 的匀强磁场,求带电粒子能到达板上的长度。
的匀强磁场,求带电粒子能到达板上的长度。
(3)若粒子的发射速率vo未知,在绝缘板的上方只加一方向垂直纸面,磁感应强度适当的匀强磁场,使粒子做圆周运动的运动半径大小恰好为d,为使同时发射出的粒子打到板上的最大时间差与(1)中相等,求vo的大小。

(1)若已知粒子的发射速率为vo,在绝缘板上方加一电场强度大小为E、方向竖直向下的匀强电场,求同一时刻发射出的带电粒子打到板上的最大时间差;
(2)若已知粒子的发射速率为vo,在绝缘板的上方只加一方向垂直纸面,磁感应强度B=
 的匀强磁场,求带电粒子能到达板上的长度。
的匀强磁场,求带电粒子能到达板上的长度。(3)若粒子的发射速率vo未知,在绝缘板的上方只加一方向垂直纸面,磁感应强度适当的匀强磁场,使粒子做圆周运动的运动半径大小恰好为d,为使同时发射出的粒子打到板上的最大时间差与(1)中相等,求vo的大小。
(1)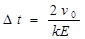 ; (2)
; (2)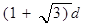 ;(3)
;(3)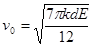
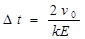 ; (2)
; (2)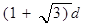 ;(3)
;(3)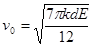
试题分析:(1)最大时间差为竖直向上和竖直向下射出的粒子,设其运动时间之差为Δt,
则:Δt=
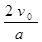 又有加速度
又有加速度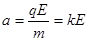 , 联立解得最大时间差为
, 联立解得最大时间差为 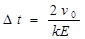
(2) 洛仑兹力充当向心力
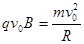
B=
 则:R =" d"
则:R =" d" 粒子运动到绝缘板的两种临界情况如图:
左侧最远处离C距离为d , 右侧离C最远处为
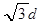
带电粒子能到达板上的长度为
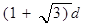
(3)设此时粒子出射速度的大小为v0
在磁场中运动时间最长和最短的粒子运动轨迹示意图如下:
由几何关系可知:
最长时间:t1=
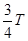 最短时间:t2=
最短时间:t2=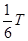
又有粒子在磁场中运动的周期
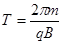
根据题意
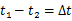 ,联立④⑤⑥⑦⑧式解得:
,联立④⑤⑥⑦⑧式解得: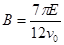
粒子在磁场中所受的洛伦兹力提供向心力
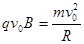 得:
得: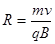
解得

练习册系列答案
相关题目
 的电子,垂直电场线飞入平行板电容器中,飞出电容器的动能为
的电子,垂直电场线飞入平行板电容器中,飞出电容器的动能为 ,如果此电子的初速度增至原来的2倍,则当它飞出电容器时的动能变为
,如果此电子的初速度增至原来的2倍,则当它飞出电容器时的动能变为 
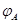 ,
,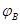 电子在A、B两点的动能分别为
电子在A、B两点的动能分别为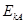 ,
,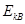 。则关于该孤立点电荷的位置及电势、电子动能大小的说法正确的是
。则关于该孤立点电荷的位置及电势、电子动能大小的说法正确的是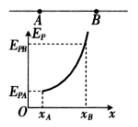
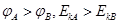

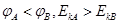
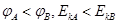

 ,再将
,再将 两板间距离先增大为2d,再减小到d/2,则微粒将 ( )
两板间距离先增大为2d,再减小到d/2,则微粒将 ( )