题目内容
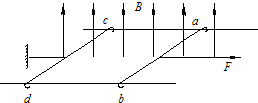如图所示，在方向竖直向上的磁感应强度为B的匀强磁场中，有两条足够长的平行金属导轨，其电阻不计，间距为L，导轨平面与磁场方向垂直．ab、cd为两根垂直导轨放置的、电阻都为R、质量都为m的金属棒．棒cd用能承受最大拉力为T0的水平细线拉住，棒cd与导轨间的最大静摩擦力为f．棒ab与导轨间的摩擦不计，在水平拉力F的作用下以加速度a由静止开始向右做匀加速直线运动，求：（1）线断以前水平拉力F随时间t的变化规律；
（2）经多长时间细线将被拉断．
分析：（1）根据速度时间公式求出速度的表达式，从而根据切割产生的感应电动势和闭合电路欧姆定律求出电流的大小，得出安培力的大小，根据牛顿第二定律求出水平拉力F随时间的变化规律．
（2）对CD棒分析，当CD棒所受的安培力等于最大静摩擦力和绳子的最大拉力时，绳子断裂，抓住共点力平衡求出细线将被拉断的时间．
（2）对CD棒分析，当CD棒所受的安培力等于最大静摩擦力和绳子的最大拉力时，绳子断裂，抓住共点力平衡求出细线将被拉断的时间．
解答：解：（1）在时刻t，棒的速度：v=a t
棒中感应电动势为：E=B L v=B L a t
棒中的感应电流为：I=
由牛顿第二定律有：F-BIL=ma
得：F=
t+ma
（2）细线拉断时满足：
BIL=f+T0
t=f+T0
解得：t=
答：（1）线断以前水平拉力F随时间t的变化规律为F=
t+ma
（2）经过t=
细线将被拉断．．
棒中感应电动势为：E=B L v=B L a t
棒中的感应电流为：I=
| BLat |
| 2R |
由牛顿第二定律有：F-BIL=ma
得：F=
| B2L2a |
| 2R |
（2）细线拉断时满足：
BIL=f+T0
| B2L2a |
| 2R |
解得：t=
| 2R(f+T0) |
| B2L2a |
答：（1）线断以前水平拉力F随时间t的变化规律为F=
| B2L2a |
| 2R |
（2）经过t=
| 2R(f+T0) |
| B2L2a |
点评：本题考查了电磁感应与力学的综合，掌握切割产生的感应电动势大小、安培力公式、闭合电路欧姆定律等知识．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，在方向竖直向下的磁感强度B=5T的匀强磁场中，水平放置两根间距d=0.1m的平行光滑直导轨，左端接有电阻R=4Ω，以及电键S和电压表（可看作理想电压表）．垂直于导轨搁置一根电阻r=1Ω的金属棒ab，棒与导轨良好接触．在电键S闭合前、后一外力均使金属棒以速度v=10m/s匀速向右移动，试求：
（2009?上海模拟）如图所示，在方向竖直向上、磁感应强度为B的匀强磁场中，有两条光滑的平行金属导轨，其电阻不计，间距为L，导轨平面与磁场方向垂直，ab、cd为垂直放置在导轨上的两根相同的金属棒，它们的电阻都为R、质量都为m，abdca构成闭合回路，cd棒用能承受最大拉力为FT的水平细线拉住，ab棒在水平拉力F的作用下以加速度a由静止开始向右做匀加速运动．
如图所示，在方向竖直向下的匀强电场中，一绝缘轻细线一端固定于O点，另一端系一带正电的小球在竖直平面内做圆周运动．小球的带电量为q，质量为m，绝缘细线长为L，电场的场强为E，若带电小球恰好能通过最高点A，则在A点时小球的速率v1为多大？小球运动到最低点B时的速率v2为多大？运动到B点时细线对小球的拉力为多大？
如图所示，在方向竖直向上的磁感应强度为B的匀强磁场中，有两条光滑的平行金属导轨，其电阻不计，间距为L，导轨平面与磁场方向垂直，ab、cd为两根垂直导轨放置的、电阻都为R、质量都为m的金属棒．棒cd用水平细线拉住，棒ab在水平拉力F的作用下以加速度a静止开始向右做匀加速运动，求：
（2005?淮安二模）如图所示，在方向竖直向下的匀强电场中，用绝缘细线拴着带负电的小球（视为质点）在竖直平面内绕O点做圆周运动，则下列判断正确的是（ ）