题目内容
如图所示,一条长为L的绝缘细线上端固定,下端拴一质量为m的带电小球,将它置于水平方向的匀强电场中,场强为E,已知当细线与竖直方向的夹角为α时,小球处于平衡位置A点,问在平衡位置以多大的速度vA释放小球,才能使之在电场中做竖直平面内的完整圆周运动？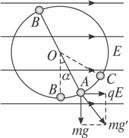
解析：小球受重力mg、电场力Eq、线的拉力T作用.简化处理,将复合场(重力场和电场)等效为重力场,小球在等效重力场中所受重力为mg′,如图：
mg′=
,即g′=
小球在A点处于平衡状态,若小球在A点以速度vA开始绕O点在竖直平面内做圆周运动,若能通过延长线上的B点(等效最高点)就能做完整的圆周运动,在B点根据向心力公式得：T+mg′=
.
T≥0为临界条件,所以vB≥
又因仅重力、电场力对小球做功,由动能定理得：-mg′
mvA2-
mvB2
由以上两式解得：vA≥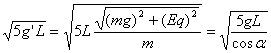
.
答案：vA=
练习册系列答案
相关题目
如图所示，一条长为L的细线，上端固定，将它置于一匀强电场中，场强大小为E，水平向右，已知当细线离开竖直位置的偏角为α时，小球处于平衡状态．
如图所示，一条长为l的细线，上端固定，下端拴一质量为m的带电小球，将它置于一匀强电场中，电场强度大小为E，方向水平向右，已知细线离开竖直位置的偏角为?时，小球处于平衡状态，则：
如图所示，一条长为L的细线，上端固定，下端栓一质量为m的带电小球，将它置于一匀强电场中，电场强度大小为E，方向水平向右，已知细线离开竖直位置的偏角为α时，小球处于平衡．
如图所示，一条长为L的细线上端固定在O点，下端系一个质量为m的小球，将它置于一个很大的方向水平向右的匀强电场中，已知小球在B点时平衡，细线与竖直线的夹角为45°，求：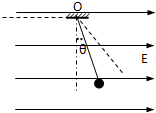
如图所示，一条长为L的细线，上端固定，将它置于一充满空间的匀强电场中，