题目内容
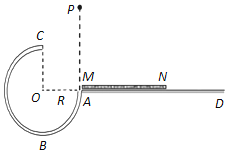
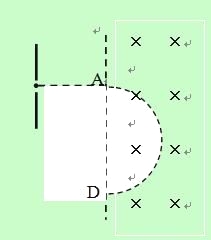
【题目】(8分)如图所示,质量为为m、电量为q的带电粒子,
经电压为U加速,又经磁感应强度为B的匀强磁场后落到图中D点,求:
(1)带电粒子在A点垂直射入磁场区域时的速率v;
(2)A、D两点间的距离l。
【答案】解:(1)带电粒子在电场中直线加速,电场力做功,动能增加,由动能定理可知,
![]() ,
,
带电粒子垂直射入磁场区域时的速率为
![]()
(2)带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力
![]() ,
,![]()
解得A、D两点间的距离![]()
【解析】
(1)粒子在电场中加速,由动能定理可以求出速度;
(2)粒子在磁场中做匀速圆周运动,由牛顿第二定律求出粒子轨道半径,然后求出距离.
(1)带电粒子在电场中直线加速,电场力做功,动能增加,
由动能定理得:qU=![]() mv2-0,
mv2-0,
解得:![]() ;
;
(2)带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:![]() ,
,
解得:![]() ,
,
A、D两点间的距离:L=2r=![]() ;
;

练习册系列答案
相关题目