题目内容
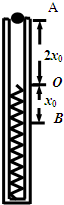 如图所示,在一直立的光滑管内放置一轻质弹簧,上端O点与管口A的距离为2x0,一质量为m的小球从管口由静止下落,将弹簧压缩至最低点B,压缩量为x0,不计空气阻力,则在上述过程中,下列说法错误的是( )
如图所示,在一直立的光滑管内放置一轻质弹簧,上端O点与管口A的距离为2x0,一质量为m的小球从管口由静止下落,将弹簧压缩至最低点B,压缩量为x0,不计空气阻力,则在上述过程中,下列说法错误的是( )分析:小球从A点释放到B点过程中:从A到O过程是自由落体;从O到B过程中先加速,到重力与弹力相等处开始减速.所以AO过程是匀加速,OB过程中加速度方向向下的大小减小的加速运动,接着加速度方向向上的大小增大的减速运动.
解答:解:A:小球由A到O做自由落体,从O开始压缩弹簧,根据胡克定律,弹簧弹力逐渐增大,根据牛顿第二定律得:a=
,加速度减小,方向向下,小球做加速度减小的加速运动,当加速度为零时,即重力和弹簧弹力相等时,速度最大;之后小球继续向下运动,弹力大于重力,做减速运动 所以A正确;
B、由A中分析知小球的最大速度在重力与受到的弹力相等处C点(在O点的下方),而小球从A到O处自由落体,由 v2=2ax得:则有v0=
=2
因此vc>vo 故B正确;
C、小球的最大速度在重力与受到的弹力相等.即mg=k△x.则k=
而△x<x0 所以k>
故C错误;
D、由于A到B处过程中,由动能定理可得:0-0=mg(2x0+x0)-E弹
解得:EP=3mgx0故D正确;
选错误得,故选C.
| mg-f |
| m |
B、由A中分析知小球的最大速度在重力与受到的弹力相等处C点(在O点的下方),而小球从A到O处自由落体,由 v2=2ax得:则有v0=
| 2g×2x0 |
| gx0 |
因此vc>vo 故B正确;
C、小球的最大速度在重力与受到的弹力相等.即mg=k△x.则k=
| mg |
| △x |
| mg |
| x0 |
D、由于A到B处过程中,由动能定理可得:0-0=mg(2x0+x0)-E弹
解得:EP=3mgx0故D正确;
选错误得,故选C.
点评:考查牛顿第二定律的同时还运用胡克定律、动能定理.让学生能熟练掌握其内容,并能巩固解题方法.本题关键是分析弹簧处于什么状态.小球的平衡点是分析的切入点.

练习册系列答案
相关题目
 如图所示,在一直立的光滑管内放置一轻质弹簧,一质量为m的小球从管口由静止下落,压缩弹簧至最低位置A,不计空气阻力,小球从接触弹簧到运动最低位置A的过程中,关于小球运动情况的下列描述正确的是( )
如图所示,在一直立的光滑管内放置一轻质弹簧,一质量为m的小球从管口由静止下落,压缩弹簧至最低位置A,不计空气阻力,小球从接触弹簧到运动最低位置A的过程中,关于小球运动情况的下列描述正确的是( )