题目内容
细线下面吊着一个质量为0.99kg的沙袋，构成一个单摆，摆长为10cm．一颗质量为10g的子弹水平射入沙袋并留在沙袋中，随沙袋一起摆动．已知沙袋摆动时摆线的最大偏角是60°，g=10m/s2，求子弹射入沙袋前的速度（ ）
分析：沙袋与子弹一起摆动的过程中机械能守恒，由机械能守恒定律可以求出子弹射入沙袋瞬间的速度．
子弹击中沙袋的过程中系统动量守恒，由动量守恒定律可以求出子弹击中沙袋前的速度．
子弹击中沙袋的过程中系统动量守恒，由动量守恒定律可以求出子弹击中沙袋前的速度．
解答：解：沙袋与子弹一起摆动的过程中，机械能守恒，则由机械能守恒定律可得：
（M+m）gL（1-cos60°）=
（M+m）v2 ，
则得：v=
=
m/s=1m/s
子弹击中木块的过程中，系统动量守恒，由动量守恒定律可得：mv0=（M+m）v，
则得：v0=
v=
×1m/s=100m/s．即子弹射入沙袋前的速度为100m/s．
故选：A
（M+m）gL（1-cos60°）=
| 1 |
| 2 |
则得：v=
| 2gL(1-cos60°) |
2×10×0.1×(1-
|
子弹击中木块的过程中，系统动量守恒，由动量守恒定律可得：mv0=（M+m）v，
则得：v0=
| M+m |
| m |
| 0.99+0.01 |
| 0.01 |
故选：A
点评：分析清楚物理过程，应用机械能守恒定律、动量守恒定律即可正确解题．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
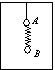在运动的升降机中天花板上用细线悬挂一个物体Ａ，下面吊着一个轻质弹簧秤（弹簧秤的质量不计），弹簧秤下吊着物体Ｂ，如图所示。物体Ａ和Ｂ的质量相等，都为m＝5kg，某一时刻弹簧秤的读数为40 N，设ｇ＝10m/s2。
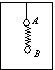在运动的升降机中天花板上用细线悬挂一个物体Ａ，下面吊着一个轻质弹簧秤（弹簧秤的质量不计），弹簧秤下吊着物体Ｂ，如图所示。物体Ａ和Ｂ的质量相等，都为m＝5kg，某一时刻弹簧秤的读数为40 N，设ｇ＝10m/s2。