题目内容
 如图所示在倾角为θ=30°的斜坡顶端A处,沿水平方向以初速度v0=10m/s抛出一小球,落在斜坡的B点,g=10m/s2,求:
如图所示在倾角为θ=30°的斜坡顶端A处,沿水平方向以初速度v0=10m/s抛出一小球,落在斜坡的B点,g=10m/s2,求:(1)小球在空中飞行的时间.
(2)AB间的距离.
分析:(1)平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,抓住位移关系求出小球在空中运动的时间.
(2)根据时间求出水平位移,从而求出AB间的距离.
(2)根据时间求出水平位移,从而求出AB间的距离.
解答:解:(1)设A到B用时为t,则有x=v0t,y=
gt2,
又有tanθ=
解得:t=
=
s.
(2)设A到B之间的距离为L,有Lcos30°=v0t
代入数据解得:L=
=
m=13.3m.
答:(1)小球在空中飞行的时间为
s.
(2)AB间的距离为13.3m.
| 1 |
| 2 |
又有tanθ=
| y |
| x |
解得:t=
| 2v0tanθ |
| g |
2
| ||
| 3 |
(2)设A到B之间的距离为L,有Lcos30°=v0t
代入数据解得:L=
| v0t |
| cosθ |
10×
| ||||
|
答:(1)小球在空中飞行的时间为
2
| ||
| 3 |
(2)AB间的距离为13.3m.
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律.属于基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示在倾角为α=30°的斜坡顶端A处,沿水平方向以初速度v0=10m/s抛出一小球,恰好落在斜坡脚的B点,求:
如图所示在倾角为α=30°的斜坡顶端A处,沿水平方向以初速度v0=10m/s抛出一小球,恰好落在斜坡脚的B点,求: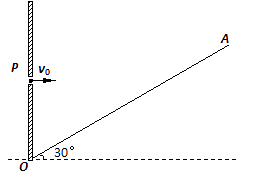 (1)粒子在磁场中做圆周运动的半径;
(1)粒子在磁场中做圆周运动的半径;

 B.
B.
 D.
D.