题目内容
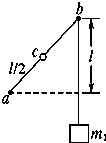 如图,墙上有两个钉子a和b,它们的连线与水平方向的夹角为45°,两者的高度差为l.一条不可伸长的轻质细绳一端固定于a点,另一端跨过光滑钉子b悬挂一质量为m1的重物.在绳上距a端l/2的c点有一固定绳圈.若绳圈上悬挂质量为m2的钩码,平衡后绳的ac段正好水平,则重物和钩码的质量比
如图,墙上有两个钉子a和b,它们的连线与水平方向的夹角为45°,两者的高度差为l.一条不可伸长的轻质细绳一端固定于a点,另一端跨过光滑钉子b悬挂一质量为m1的重物.在绳上距a端l/2的c点有一固定绳圈.若绳圈上悬挂质量为m2的钩码,平衡后绳的ac段正好水平,则重物和钩码的质量比| m1 | m2 |
分析:根据题意画出平衡后的物理情景图.
对绳子上c点进行受力分析.根据几何关系找出BC段与水平方向的夹角.
根据平衡条件和三角函数表示出力与力之间的关系.
对绳子上c点进行受力分析.根据几何关系找出BC段与水平方向的夹角.
根据平衡条件和三角函数表示出力与力之间的关系.
解答: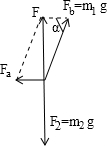 解:对绳子上c点进行受力分析:
解:对绳子上c点进行受力分析:
平衡后设绳的BC段与水平方向成α角,根据几何关系有:
tanα=2,sinα=
.
对结点C分析,将Fa和Fb合成为F,根据平衡条件和三角函数关系得:
F2=m2g=F,Fb=m1g.
sinα=
=
所以得:
=
=
故答案为:
.
 解:对绳子上c点进行受力分析:
解:对绳子上c点进行受力分析:平衡后设绳的BC段与水平方向成α角,根据几何关系有:
tanα=2,sinα=
| 2 | ||
|
对结点C分析,将Fa和Fb合成为F,根据平衡条件和三角函数关系得:
F2=m2g=F,Fb=m1g.
sinα=
| F |
| Fb |
| m2 |
| m1 |
所以得:
| m1 |
| m2 |
| 1 |
| sinα |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:该题的关键在于能够对线圈进行受力分析,利用平衡状态条件解决问题.
力的计算离不开几何关系和三角函数.
力的计算离不开几何关系和三角函数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
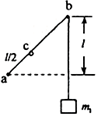 (2011?海南)如图,墙上有两个钉子a和b,它们的连线与水平方向的夹角为45°,两者的高度差为l.一条不可伸长的轻质细绳一端固定于a点,另一端跨过光滑钉子b悬挂一质量为m1的重物.在绳子距a端
(2011?海南)如图,墙上有两个钉子a和b,它们的连线与水平方向的夹角为45°,两者的高度差为l.一条不可伸长的轻质细绳一端固定于a点,另一端跨过光滑钉子b悬挂一质量为m1的重物.在绳子距a端 得c点有一固定绳圈。若绳圈上悬挂质量为m2的钩码,平衡后绳的ac段正好水平,则重物和钩码的质量比
得c点有一固定绳圈。若绳圈上悬挂质量为m2的钩码,平衡后绳的ac段正好水平,则重物和钩码的质量比 为( )
为( )
 B. 2
B. 2 D.
D.
 得c点有一固定绳圈。若绳圈上悬挂质量为m2的钩码,平衡后绳的ac段正好水平,则重物和钩码的质量比
得c点有一固定绳圈。若绳圈上悬挂质量为m2的钩码,平衡后绳的ac段正好水平,则重物和钩码的质量比 为
为
 B. 2 C.
B. 2 C. D.
D.
