题目内容
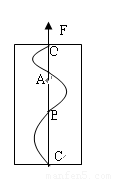
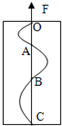 如图所示,一块涂有炭黑的玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上做匀加速运动.一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃上画出了图示曲线,量得OA=1cm,OB=4cm,OC=9cm,求外力F的大小.(g取10m/s2)
如图所示,一块涂有炭黑的玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上做匀加速运动.一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃上画出了图示曲线,量得OA=1cm,OB=4cm,OC=9cm,求外力F的大小.(g取10m/s2)
解:在力F作用下,玻璃板向上作匀加速运动,图示OC间曲线所反映出的是振动的音叉振动位移随时间变化的规律,其中直线OC代表音叉振动1.5个周期内玻璃板运动的位移,而OA、AB、BC间对应的时间均为0.5个周期,即t= =
=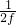 =0.1s.故可利用匀加速直线运动的规律--连续相等时间内的位移差等于恒量即△x=aT2来求加速度.
=0.1s.故可利用匀加速直线运动的规律--连续相等时间内的位移差等于恒量即△x=aT2来求加速度.
设板竖直向上的加速度为a,则有:
sBA-sAO=aT2
即 sBO-sAO-sAO=aT2…①
其中T=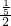 s=0.1s…②
s=0.1s…②
由牛顿第二定律得
F-mg=ma…③
解①②③可求得:F=24N.
答:外力F的大小为24N.
分析:从固定电动音叉在玻璃上画出的曲线看出OA、AB、BC间对应的时间均为半个周期,玻璃板又做匀加速运动,根据匀变速直线运动的推论△x=aT2求出加速度,再由牛顿第二定律求解外力F的大小.
点评:本题一要抓住音叉振动与玻璃板运动的同时性,OA、AB、BC对应于音叉振动半个周期.二是利用打点计时器测加速度的原理求解加速度.
 =
=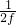 =0.1s.故可利用匀加速直线运动的规律--连续相等时间内的位移差等于恒量即△x=aT2来求加速度.
=0.1s.故可利用匀加速直线运动的规律--连续相等时间内的位移差等于恒量即△x=aT2来求加速度.设板竖直向上的加速度为a,则有:
sBA-sAO=aT2
即 sBO-sAO-sAO=aT2…①
其中T=
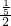 s=0.1s…②
s=0.1s…②由牛顿第二定律得
F-mg=ma…③
解①②③可求得:F=24N.
答:外力F的大小为24N.
分析:从固定电动音叉在玻璃上画出的曲线看出OA、AB、BC间对应的时间均为半个周期,玻璃板又做匀加速运动,根据匀变速直线运动的推论△x=aT2求出加速度,再由牛顿第二定律求解外力F的大小.
点评:本题一要抓住音叉振动与玻璃板运动的同时性,OA、AB、BC对应于音叉振动半个周期.二是利用打点计时器测加速度的原理求解加速度.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图所示,一块涂有炭黑的玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上做匀加速运动.一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃上画出了图示曲线,量得OA=1cm,OB=4cm,OC=9cm,求外力F的大小.(g取10m/s2)
如图所示,一块涂有炭黑的玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上做匀加速运动.一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃上画出了图示曲线,量得OA=1cm,OB=4cm,OC=9cm,求外力F的大小.(g取10m/s2)