题目内容
【题目】质量为M=3kg的平板车放在光滑的水平面上,在平板车的最左端有一小物块(可视为质点),物块的质量为m=1kg,小车左端上方如图所示固定着一障碍物A,初始时,平板车与物块一起以水平速度v0=2m/s向左运动,当物块运动到障碍物A处时与A发生无机械能损失的碰撞,而小车继续向左运动,取重力加速度g=10m/s2.
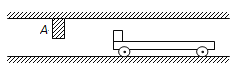
(1)设平板车足够长,求物块与障碍物第一次碰撞后,物块与平板车所能获得的共同速度;
(2)设平板车足够长,物块与障碍物第一次碰撞后,物块向右运动对地所能达到的最大距离是s=0.4m,求物块与A第一次碰撞后到第二次碰撞前相对小车滑动的距离.
【答案】(1)1m/s(2)1.2m
【解析】(1)以物块和车为系统,由动量守恒定律得:
![]()
代入已知数据解得,共同速度:v=1m/s
(2)设物块受到的摩擦力为f,对物块由动能定理得:
![]()
代入已知数据解得:f=5N
物块与A第二次碰撞前已与车保持相对静止,对系统由能量守恒定律得:
![]()
代入已知数据解得:s相对=1.2m
点睛; 本题综合考查了动能定理、动量守恒定律和能量守恒定律,综合性较强,对学生能力要求较高,需加强这方面的训练.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目