题目内容
用活塞式抽气机抽气，在温度不变的情况下，从玻璃瓶中抽气，第一次抽气后，瓶内气体的压强减小到原来的
，要使容器内剩余气体的压强减为原来的
，抽气次数应为（ ）
| 4 |
| 5 |
| 256 |
| 625 |
分析：在抽气过程中气体温度不变，由玻意耳定律列方程，可以求出抽气的次数．
解答：解：设玻璃瓶的容积是V，抽气机的容积是V0，
气体发生等温变化，由玻意耳定律可得：
PV=
P（V+V0），V0=
V，
设抽n次后，气体压强变为原来的
，
由玻意耳定律可得：
抽一次时：PV=P1（V+V0），P1=
P，
抽两次时：P1V=P2（V+V0），P2=(
)2P，
抽n次时：Pn=(
)nP，Pn=
P，则n=4，
故选C．
气体发生等温变化，由玻意耳定律可得：
PV=
| 4 |
| 5 |
| 1 |
| 4 |
设抽n次后，气体压强变为原来的
| 256 |
| 625 |
由玻意耳定律可得：
抽一次时：PV=P1（V+V0），P1=
| 4 |
| 5 |
抽两次时：P1V=P2（V+V0），P2=(
| 4 |
| 5 |
抽n次时：Pn=(
| 4 |
| 5 |
| 256 |
| 625 |
故选C．
点评：气体发生等温变化时，遵守玻意耳定律，应用玻意耳定律列方程，即可求出抽气次数．
练习册系列答案
相关题目
，要使容器内剩余气体的压强减为原来的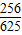
，抽气次数应为（ ）