题目内容
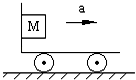
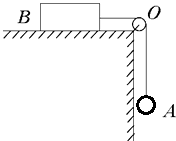
【题目】如图所示,传送带与水平成α=37°,传送带A、B间距L=5.8m,传送带始终以4m/s速度顺时针转动,将一小物体轻轻释放在A处,小物体与传送带间动摩擦因数为μ=0.5.(sin37°=0.6,cos37°=0.8)(取g=10m/s2)试求:
(1)刚释放时,小物体加速度的大小?
(2)小物体从A运动到B所需时间?
【答案】
(1)解:受力分析:正交分解,
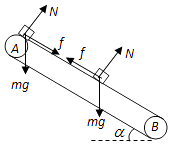
根据牛顿第二定律可知:mgsinα+μmgcosα=ma1
解得a1=gsinα+μgcosα=10m/s2
答:刚释放时,小物体加速度的大小为10m/s2
(2)解:物块加速到4 m/s的位移 ![]() m<L,
m<L,
运动的时间 ![]()
又因μ=0.5<tanα,故物块先以a1加速,再以 ![]() m/s2
m/s2
加速通过的位移为
x2=L﹣x1=5m,
根据位移时间公式可知 ![]() ,
,
解得:t2=1s或t2=﹣5s(舍)
经历的总时间为t=t1+t2=1.4s
答:小物体从A运动到B所需时间为1.4s
【解析】物体放在传送带上后,开始阶段,传送带的速度大于物体的速度,传送带给物体一沿斜面向下的滑动摩擦力,物体由静止开始加速下滑,当物体加速至与传送带速度相等时,由于μ<tanθ,物体在重力作用下将继续加速,此后物体的速度大于传送带的速度,传送带给物体沿传送带向上的滑动摩擦力,但合力沿传送带向下,物体继续加速下滑,综上可知,滑动摩擦力的方向在获得共同速度的瞬间发生了“突变”.
【考点精析】本题主要考查了滑动摩擦力和静摩擦力的相关知识点,需要掌握滑动摩擦力:利用公式f=μF N 进行计算,其中FN 是物体的正压力,不一定等于物体的重力,甚至可能和重力无关.或者根据物体的运动状态,利用平衡条件或牛顿定律来求解;静摩擦力:静摩擦力大小可在0与fmax 之间变化,一般应根据物体的运动状态由平衡条件或牛顿定律来求解才能正确解答此题.

【题目】某物理兴趣小组利用传感器进行探究实验,其实验装置及原理图分别如甲、乙所示.
该装置中,A、B为力传感器,研究对象是质量m=310g的金属圆柱体G,将G放在A、B的两探头之间,两探头受到压力的数据,通过传感器、数据采集器传输给计算机,数据如表1所示.
表1 圆柱体的质量:310g
θ/° | 0 | 30 | 45 | 60 | 90 |
FA/N | 0.00 | 1.49 | 2.12 | 2.59 | 3.02 |
FB/N | 3.01 | 2.61 | 2.13 | 1.50 | 0.00 |
(1)观察、分析数据表1,可得出:金属圆柱体重力沿斜面向下的分力FA随斜面倾角θ的增大而 , 垂直斜面向下的分力FB随斜面倾角θ的增大而 .
(2)某同学发现两传感器的读数并不是与角度的变化成正比,他猜想圆柱体所受重力及其分力间满足某个函数关系,并根据该函数关系计算两探头受到压力的理论值如表2所示(g取9.8m/s2)
表2 圆柱体的质量:310g
θ/° | 0 | 30 | 45 | 60 | 90 |
FA/N | 0.00 | 1.52 | 2.15 | 2.63 | 3.04 |
FB/N | 3.04 | 2.63 | 2.15 | 1.52 | 0.00 |
该同学猜测的函数关系式应当分别为:FA= , FB=(用金属圆柱体质量m、重力加速度g、斜面倾角θ表示)
(3)在实验中无论是分析“表1”还是“表2”的数据时,都认为传感器的读数都等于相应的圆柱体重力的分力,其物理学依据是(乙沿斜面方向为例);因为A传感器的读数等于A传感器所受的压力,根据此压力大小等于圆柱体沿斜面方向所受的支持力,而根据此支持力大小等于圆柱体重力沿斜面方向的分力
(4)为了减少实验误差,可采取的办法是(写出一个即可)