题目内容
1. 如图所示,用一块长L1=2.5m的木板(木板下端有一底座高度与木板A、B相同)在墙和地面间架设斜面,斜面与水平地面的倾角θ可在0~60°间调节后固定.将质量m1=5kg的小物块从斜面顶端静止释放,为避免小物块与地面发生撞击,在地面上紧靠轨道依次排放两块完全相同的木板A、B,长度均为l=2m,质量均为m2=10kg(忽略小物块在转角处和底座运动的能量损失).物块与斜面间的动摩擦因数μ=0.125,物块与木板间的动摩擦因数μ1=0.4,木板与地面间的动摩擦因数μ2=0.1(最大静摩擦力等于滑动摩擦力;重力加速度g=10m/s2)
如图所示,用一块长L1=2.5m的木板(木板下端有一底座高度与木板A、B相同)在墙和地面间架设斜面,斜面与水平地面的倾角θ可在0~60°间调节后固定.将质量m1=5kg的小物块从斜面顶端静止释放,为避免小物块与地面发生撞击,在地面上紧靠轨道依次排放两块完全相同的木板A、B,长度均为l=2m,质量均为m2=10kg(忽略小物块在转角处和底座运动的能量损失).物块与斜面间的动摩擦因数μ=0.125,物块与木板间的动摩擦因数μ1=0.4,木板与地面间的动摩擦因数μ2=0.1(最大静摩擦力等于滑动摩擦力;重力加速度g=10m/s2)(1)当θ角增大到多少时,小物块能从斜面开始下滑?(用正切值表示)
(2)当θ增大到37°时,通过计算判断货物是否会从木板B的右端滑落?若能,求货物滑离木板B右端时的速度;若不能,求货物最终停在B板上的位置?(已知sin37°=0.6,cos37°=0.8)
分析 (1)对木块由共点力平衡条件进行分析,则可求得动摩擦因数;
(2)分析θ=37°时物体在斜面上的运动情况,由动能定理求解到达A板左侧的速度;再分析木板在A上的运动,最后假设不能从B中滑出,由功能关系列式进行分析求解.
解答 解:(1)对小物块有:
mgsinθ=μmgcosθ
解得:tanθ=μ=0.125
(2)当θ=37°时,物块沿斜面下滑,
由动能定理可知:
(mgsinθ-μmgcosθ)L1=$\frac{1}{2}$mv02-0
解得v0=5m/s当物块滑上木板时,木板为静止状态,所以物块在木板A上做匀减速运动,设物块滑上木板B的速度为v1
则有:-m1gl=$\frac{1}{2}$m1v12-$\frac{1}{2}$m1v02
解得:v1=3m/s
物块滑上木板B后,由于物块给木板的摩擦力大于地面给木板B的摩擦力,所以木板B滑动,设最后两者达到共速;
对物块有:
v共=v1-μ1gt
x1=$\frac{{v}_{1}+{v}_{共}}{2}t$
对木板B:
μ1m1g-μ2(m1+m2)g=m2a
v共=at
x2=$\frac{{v}_{共}}{2}t$
则△x=x1-x2=1m<l
故假设成立;
物块最终停在木板B的中点处.
答:(1)当tanθ=μ=0.125时,物体开始下滑;
(2)物体最终停在木板B的中点处.
点评 本题考查动能定理及牛顿第二定律的应用,要注意明确研究对象,做好各过程的受力分析,明确物理规律的正确应用才能准确解题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
9. “旋转秋千”是游乐园里常见的游乐项目,其基本装置是将绳子上端固定在转盘的边上,绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看质点,“旋转秋千”可简化为如图所示的模型.图中“旋转秋千”的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上.不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法正确的是( )
“旋转秋千”是游乐园里常见的游乐项目,其基本装置是将绳子上端固定在转盘的边上,绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看质点,“旋转秋千”可简化为如图所示的模型.图中“旋转秋千”的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上.不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法正确的是( )
 “旋转秋千”是游乐园里常见的游乐项目,其基本装置是将绳子上端固定在转盘的边上,绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看质点,“旋转秋千”可简化为如图所示的模型.图中“旋转秋千”的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上.不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法正确的是( )
“旋转秋千”是游乐园里常见的游乐项目,其基本装置是将绳子上端固定在转盘的边上,绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看质点,“旋转秋千”可简化为如图所示的模型.图中“旋转秋千”的两个座椅A、B质量相等,通过相同长度的缆绳悬挂在旋转圆盘上.不考虑空气阻力的影响,当旋转圆盘绕竖直的中心轴匀速转动时,下列说法正确的是( )| A. | A的速度比B的大 | |
| B. | A与B的向心加速度大小相等 | |
| C. | 悬挂A、B的缆绳与竖直方向的夹角相等 | |
| D. | 悬挂A的缆绳所受的拉力比悬挂B的小 |
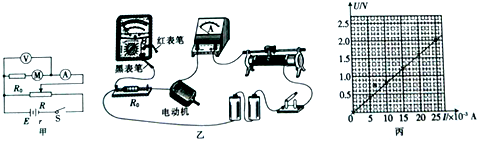
16. 如图所示,一倾斜角为30°的匀质圆盘绕垂直于盘面的固定对称轴以恒定角速度ω=1rad/s转动,盘面上离转轴距离d=2.5m处有一小物体与圆盘始终保持相对静止.则物体与盘面间的动摩擦因数至少为(设最大静摩擦力等于滑动摩擦力,g取10m/s2)( )
如图所示,一倾斜角为30°的匀质圆盘绕垂直于盘面的固定对称轴以恒定角速度ω=1rad/s转动,盘面上离转轴距离d=2.5m处有一小物体与圆盘始终保持相对静止.则物体与盘面间的动摩擦因数至少为(设最大静摩擦力等于滑动摩擦力,g取10m/s2)( )
 如图所示,一倾斜角为30°的匀质圆盘绕垂直于盘面的固定对称轴以恒定角速度ω=1rad/s转动,盘面上离转轴距离d=2.5m处有一小物体与圆盘始终保持相对静止.则物体与盘面间的动摩擦因数至少为(设最大静摩擦力等于滑动摩擦力,g取10m/s2)( )
如图所示,一倾斜角为30°的匀质圆盘绕垂直于盘面的固定对称轴以恒定角速度ω=1rad/s转动,盘面上离转轴距离d=2.5m处有一小物体与圆盘始终保持相对静止.则物体与盘面间的动摩擦因数至少为(设最大静摩擦力等于滑动摩擦力,g取10m/s2)( )| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
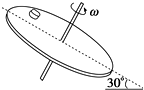
7. 如图,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置-时间(x-t)图线.由图可知( )
如图,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置-时间(x-t)图线.由图可知( )
 如图,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置-时间(x-t)图线.由图可知( )
如图,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置-时间(x-t)图线.由图可知( )| A. | 在时刻t1,a 车追上b车 | |
| B. | 在时刻t2,a、b两车运动方向相反 | |
| C. | 在t1到t2这段时间内,b车的位移比a车的大 | |
| D. | 在t1 到t2这段时间内,b车的速率一直比a车的大 |
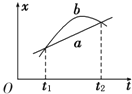
5.2012年11月,“歼15”舰载机在“辽宁号”航空母舰上着舰成功.图(a)为利用阻拦系统让舰载机在飞行甲板上快速停止的原理示意图.飞机着舰并成功钩住阻拦索后,飞机的动力系统立即关闭,阻拦系统通过阻拦索对飞机施加一作用力,使飞机在甲板上短距离滑行后停止.某次降落,以飞机着舰为计时零点,飞机在t=0.4s时恰好钩住阻拦索中间位置,其着舰到停止的速度一时间图线如图(b)所示.假如无阻拦索,飞机从着舰到停止需要的滑行距离约为1 000m.已知航母始终静止,重力加速度的大小为g.则( )

| A. | 在0.4s~2.5s时问内,阻拦索的张力几乎不随时间变化 | |
| B. | 从着舰到停止,飞机在甲板上滑行的距离约为无阻拦索时的$\frac{1}{10}$ | |
| C. | 在滑行过程中,飞行员所承受的加速度大小不会超过2.5g | |
| D. | 在0.4s~2.5s时间内,阻拦系统对飞机做功的功率逐渐减小 |
 我国的最新交通规则规定:黄灯亮时车头已越过停车线的车辆可以继续通行,车头未越过停车线的若继续前行则视为闯黄灯,属于交通违章行为,我国一般城市路口红灯变亮之前绿灯和黄灯各有3s的闪烁时间.国家汽车检测标准中有关汽车制动初速度与刹车距离的规定是这样的:小客车在制动初速度为14m/s的情况下,制动距离不得大于20m.
我国的最新交通规则规定:黄灯亮时车头已越过停车线的车辆可以继续通行,车头未越过停车线的若继续前行则视为闯黄灯,属于交通违章行为,我国一般城市路口红灯变亮之前绿灯和黄灯各有3s的闪烁时间.国家汽车检测标准中有关汽车制动初速度与刹车距离的规定是这样的:小客车在制动初速度为14m/s的情况下,制动距离不得大于20m.