题目内容
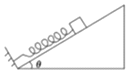
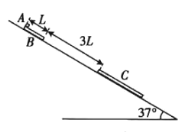
【题目】如图所示,倾角![]() =37°的足够长斜面上有一长为L、质量为2m的木板B,木板B上端有一质量为m的滑块A(视为质点),木板下端3L处有一质量为m的足够长木板C锁定。在斜面上,滑块A与木板B、C间的动摩擦因数均为μ1=0.25,木板C与斜面间无摩擦,木板B、C的厚度相同。现同时由静止释放A、B,在B与C碰撞前瞬间,解除对C的锁定,此时A恰好滑离B而滑上C,已知B、C碰撞为弹性碰撞,重力加速度为g,sin 37° = 0.6, cos 37°=0.8,求:
=37°的足够长斜面上有一长为L、质量为2m的木板B,木板B上端有一质量为m的滑块A(视为质点),木板下端3L处有一质量为m的足够长木板C锁定。在斜面上,滑块A与木板B、C间的动摩擦因数均为μ1=0.25,木板C与斜面间无摩擦,木板B、C的厚度相同。现同时由静止释放A、B,在B与C碰撞前瞬间,解除对C的锁定,此时A恰好滑离B而滑上C,已知B、C碰撞为弹性碰撞,重力加速度为g,sin 37° = 0.6, cos 37°=0.8,求:
(1)木板B与斜面间的动摩擦因数μ2;
(2)B、C发生碰撞后瞬间,木板C的速度大小vC;
(3)B、C发生碰撞后2s时,滑块A到木板C上端的距离x。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)0。
;(3)0。
【解析】
(1)当滑块A在木板B上滑动时,对A受力分析有
![]()
即aA=0.4g
在B与C碰撞前瞬间,滑块A做匀变速直线运动有
![]()
对木板B受力分析有
![]()
即aB=(0.7-1.2μ2)g
在B与C碰撞前瞬间,木板B做匀变速直线运动有
![]()
解得![]() 。
。
(2)设B、C发生弹性碰撞前瞬间木板B的速度大小为vB,有
![]()
解得![]()
B、C发生弹性碰撞时动量守恒:
![]()
由弹性碰撞可知碰撞前后动能之和相等:
![]()
解得B、C发生碰撞后木板C的速度大小![]() 。
。
(3)B、C发生弹性碰撞前瞬间,滑块A的速度
![]()
由于C碰撞后速度与A相同且C与斜面间无摩擦,所以A、C不发生相对滑动,以相同加速度沿斜面向下运动,滑块A到木板C上端的距离始终为x=0。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在探究弹簧的弹力与伸长量之间关系的实验中,所用装置如图甲所示,将轻弹簧的一端固定,另一端与力传感器连接,其伸长量通过刻度尺测得,某同学的实验数据列于下表中:


伸长量 | 2.00 | 4.00 | 6.00 | 8.00 | 10.00 |
弹力 | 1.50 | 2.93 | 4.55 | 5.98 | 7.50 |
(1)以![]() 为横坐标,
为横坐标,![]() 为纵坐标,在图乙的坐标纸上描绘出能正确反映这一弹簧的弹力与伸长量之间的关系图线(_______)
为纵坐标,在图乙的坐标纸上描绘出能正确反映这一弹簧的弹力与伸长量之间的关系图线(_______)
(2)由图线求得这一弹簧的劲度系数为________.(保留三位有效数字)