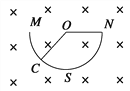题目内容
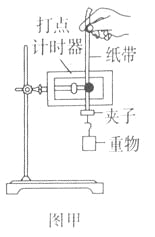
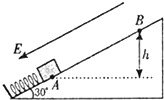
【题目】如图所示，圆环A的质量 m1=10kg，被销钉固定在竖直光滑的杆上，杆固定在地面上，A与定滑轮等高，A与定滑轮的水平距离L＝3m，不可伸长的细线一端系在A上，另一端通过定滑轮系系在小物体B上，B的质量m2＝2kg，B的另一侧系在弹簧上，弹簧的另一端系在固定在斜面底端挡板C上，弹簧的劲度系数k＝40N/m，斜面的倾角θ＝30°，B与斜面的摩擦因数μ＝
/3，足够的长的斜面固定在地面上，B受到一个水平向右的恒力F作用，F=20N，开始时细线恰好是伸直的，但未绷紧，B是静止的，弹簧被压缩。拔出销钉，A开始下落，当A下落h＝4m时，细线断开、B与弹簧脱离、恒力F消失，不计滑轮的摩擦和空气阻力。问:
（1）销钉拔出前，画出物体B的受力示意图，此时弹簧的压缩量
（2）当A下落h＝4m时，A、B两个物体速度大小的关系
（3）B在斜面上运动的最大距离？（g＝10m/s2）
【答案】（1）
（2）
（3）
,
【解析】（1）对物体受力分析可得受力图 :
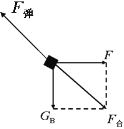
F和重力的合力
， 
的方向平行斜面向下
由题意分析可得物体对斜面的压力为0 故摩擦力为0
由平衡条件
：
弹簧的压缩量 
（2设当滑块下
时,环和物的速度分别为v1 , v2. 此时物体上升的距离
由运动的分解和几何关系得：
（3）由于弹簧的压缩量和伸长量相同，弹簧对物体做功为零
对系统用动能定理：
当细线断开、B与弹簧脱离、恒力F消失后
对物体B受力分析，由牛顿定律：
,
练习册系列答案
相关题目
