题目内容
如图甲所示,截面积为0.2m2的100匝圆形线圈A处在变化磁场中,磁场方向垂直线圈截面,其磁感应强度B随时间t的变化规律如图乙所示.设向外为B的正方向,线圈A上的箭头为感应电流I的正方向,R1=4Ω,R2=6Ω,C=30μF,线圈内阻不计.求电容器充电时的电压和2s后电容器放电的电量. 其中通过R2的电量是多少?


分析:(1)根据E=n
求出感应电动势的大小,再根据闭合电路欧姆定律求出电流的大小,从而求出电容器充电时的电压.
(2)求出闭合S后,根据Q=CU求出电容器所带的电量,根据电阻的阻值与电量成反比关系,即可确定通过R2的电量.
| △BS |
| △t |
(2)求出闭合S后,根据Q=CU求出电容器所带的电量,根据电阻的阻值与电量成反比关系,即可确定通过R2的电量.
解答:解:磁感应强度的变化率为:
=
T/s=0.02 T/s,
感应电动势为:E=n
t=nS
=100×0.2×0.02V=0.4 V
通过R2的电流强度为:I=
=
A=0.04 A,
所以:UC=IR2=0.04×6V=0.24V,
2 s后磁场消失(B=0),电容器通过电阻和线圈放电;
放电的电量即为充电后电容器上的带电量,
所以:Q=CUC=30×10-6×0.24C=7.2×10-6 C.
其中通过R2的电量是总电量的
,QR2=1.44×10-6 C.
答:电容器充电时的电压0.24V,和2s后电容器放电的电量7.2×10-6 C,其中通过R2的电量是1.44×10-6 C.
| △B |
| △t |
| 0.02 |
| 1 |
感应电动势为:E=n
| △? |
| △t |
| △B |
| △t |
通过R2的电流强度为:I=
| E |
| R1+R2 |
| 0.4 |
| 4+6 |
所以:UC=IR2=0.04×6V=0.24V,
2 s后磁场消失(B=0),电容器通过电阻和线圈放电;
放电的电量即为充电后电容器上的带电量,
所以:Q=CUC=30×10-6×0.24C=7.2×10-6 C.
其中通过R2的电量是总电量的
| 2 |
| 5 |
答:电容器充电时的电压0.24V,和2s后电容器放电的电量7.2×10-6 C,其中通过R2的电量是1.44×10-6 C.
点评:解决本题的关键掌握法拉第电磁感应定律,以及会运用闭合电路欧姆定律计算感应电流的大小,并掌握电量 Q=CUC公式.同时掌握当与电容器的并联时,则电容器放电电量与阻值成反比.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
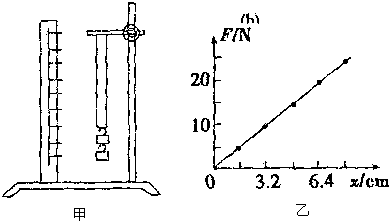 橡皮筋也像弹簧一样,在弹性限度内,伸长量x与弹力F成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度L、横截面积S有关.理论和实践都表明k=YS/L,其中Y是一个由材料决定的常数,材料力学中称之为杨氏模量
橡皮筋也像弹簧一样,在弹性限度内,伸长量x与弹力F成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度L、横截面积S有关.理论和实践都表明k=YS/L,其中Y是一个由材料决定的常数,材料力学中称之为杨氏模量
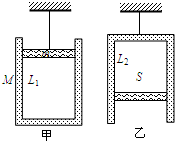 一圆柱形气缸,质量为M,总长度为L,内有一厚度不计的活塞,质量为m、截面积为S,活塞与气缸壁间摩擦不计,但不漏气,温度为t0时,如果用绳子系住活塞将气缸悬挂起来,如图甲所示,气缸内气体柱的高为L1,如果用绳子系住气缸底,将气缸倒过来悬挂起来,如图乙所示,气缸内气体柱的高为L2,设两种情况下气缸都处于竖直状态,求:
一圆柱形气缸,质量为M,总长度为L,内有一厚度不计的活塞,质量为m、截面积为S,活塞与气缸壁间摩擦不计,但不漏气,温度为t0时,如果用绳子系住活塞将气缸悬挂起来,如图甲所示,气缸内气体柱的高为L1,如果用绳子系住气缸底,将气缸倒过来悬挂起来,如图乙所示,气缸内气体柱的高为L2,设两种情况下气缸都处于竖直状态,求: